

Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.



Đáp án B.
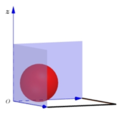
Phương pháp giải: Gắn hệ tọa độ Oxyz, tìm bán kính quả bóng chính là bán kính của mặt cầu
Lời giải: Xét quả bóng tiếp xúc với các bức tường và chọn hệ trục Oxyz như hình vẽ bên (tương tự với góc tường còn lại).
Gọi I(a;a;a) là tâm của mặt cầu (tâm quả bóng) và R = a
=> phương trình mặt cầu của quả bóng là ![]()
Giả sử M(x;y;z) nằm trên mặt cầu (bề mặt của quả bóng) sao cho d(M;(Oxy)) = 1; d(M;(Oyz)) = 2; d(M;(Oxz)) = 3
Khi đó z = 1; x = 2; y = 3 => M(2;3;1) ∈ (S) (2).
Từ (1),(2) suy ra ![]()
=>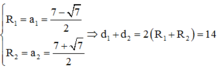

Chọn đáp án B
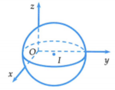
Hai bức tường và nền nhà mà quả bóng tiếp xúc tạo thành một hệ trục tọa độ Oxyz như hình vẽ. Mỗi quả bóng coi như một mặt cầu có tâm I a ; b ; c
Vì mỗi quả bóng đều tiếp xúc với hai bức tường và nền nhà nên chúng tiếp xúc với ba mặt phẳng tọa độ O x y , O y z v à O x z
Tức là
![]()
![]()
Suy ra I a ; a ; a
Gọi M x ; y ; z là điểm nằm trên quả bóng có khoảng cách đến hai bức tường và nền nhà mà nó tiếp xúc bằng 1, 2, 4
Suy ra M 1 ; 2 ; 4
Điểm M nằm trên quả bóng khi
![]()
![]()
Phương trình (*) có ∆ ' = 7 > 0 nên có hai nghiệm a 1 , a 2 và a 1 + a 2 = 7 (theo định lý Vi-ét). Khi đó tổng đường kính của hai quả bóng là
2 a 1 + a 2 = 14

Đường kính quả bóng tennis là
2R = 25 5 = 5.
Diện tích quả bóng:
S = 4 π . R 2 = 4 π . 5 2 2 = 25 π c m 2
Đáp án B

Đáp án C
Gọi S là tổng quãng đường bóng đã bay, khi đó ta có:
S = 3 + 3. 2 3 .3 2 3 2 + 3. 2 3 3 + 3. 2 3 4 + 3. 2 3 5 + ... + 3. 2 3 n + ...
S là tổng của cấp số nhân lùi vô hạn có số hạng đầu tiên là u 1 = 3 , công bội là q = 2 3 nên
S = u 1 1 − q = 3 1 − 2 3 = 9
Vậy tổng quãng đường đã bay của bóng là khoảng 9m.

Đáp án C
Tổng khoảng cách cần tìm là (với n ∈ R * )
S
=
81
+
2
.
81
.
2
3
+
2
.
81
.
2
3
2
+
.
.
.
+
2
.
81
.
2
3
n
+
1
=
81
+
2
.
81
.
2
3
+
81
.
2
3
2
+
.
.
.
+
81
.
2
3
n
+
1
+
.
.
.
Do 81 . 2 3 + 81 . 2 3 2 + . . . + 81 . 2 3 n + 1 + . . . l
à tổng của cấp số nhân lùi vô hạn với
u 1 = 81 . 2 3 = 54 q = 2 3 ⇒ S = 81 + 2 . u 1 1 - q = 405 m