Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Rút ra một lá bài gồm 52 lá .Xác suất để rút được 2 lá chất cơ là
Giải giúp mình với ạ .Mình cảm ơn.

-n(Ω)= 52
-n(A): 13C2 (1 bộ bài 52 lá có 13 lá chất cơ, rút ra 2 lá)
-P(A): 13C2 /52 = 3/2
ko biết đúgn ko lâu r ko làm +))

Không gian mẫu: \(\dfrac{52!}{\left(4!\right)^{13}}\)
Do đó xác suất: \(P=\dfrac{1}{\dfrac{52!}{\left(4!\right)^{13}}}=\dfrac{\left(4!\right)^{13}}{52!}=...\)
1.
ĐKXĐ: \(-3\le x\le1\)
\(2\left(x+3\right)-m\sqrt{x+3}+5\left(1-x\right)+2m\sqrt{1-x}=4\sqrt{\left(x+3\right)\left(1-x\right)}\)
\(\Leftrightarrow m\left(2\sqrt{1-x}-\sqrt{x+3}\right)=3x-11+4\sqrt{\left(x+3\right)\left(1-x\right)}\)
Đặt \(2\sqrt{1-x}-\sqrt{x+3}=t\Rightarrow t\in\left[-2;4\right]\)
\(t^2=7-3x-4\sqrt{\left(1-x\right)\left(x+3\right)}\)
\(\Rightarrow3x-11+4\sqrt{\left(1-x\right)\left(x+3\right)}=-4-t^2\)
Do đó pt trở thành: \(m.t=-t^2-4\)
- Với \(t=0\) ko phải nghiệm
- Với \(t\ne0\Rightarrow m=\dfrac{-t^2-4}{t}\)
Xét \(f\left(t\right)=\dfrac{-t^2-4}{t}\) với \(t\in\left[-2;4\right]\)
\(f^2\left(t\right)=\dfrac{\left(t^2+4\right)^2}{t^2}\ge4\Rightarrow\left[{}\begin{matrix}f\left(t\right)\le-2\\f\left(t\right)\ge2\end{matrix}\right.\)
\(\Rightarrow\left[{}\begin{matrix}m\le-2\\m\ge2\end{matrix}\right.\)

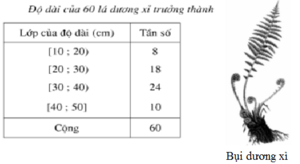
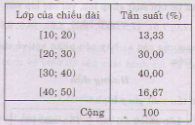
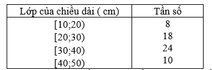
a) Bảng phân bố tần suất ghép lớp:
| Lớp của chiều dài (cm) | Tần suất |
|---|---|
| [10; 20) | 13,3 |
| [20; 30) | 30,0 |
| [30; 40) | 40,0 |
| [40; 50) | 16,7 |
| Cộng | 100 (%) |
b) Tỉ lệ lá có chiều dài dưới 30 cm là:
13,3 + 30 = 43,3 %
Tỉ lệ lá có chiều dài từ 30 cm đến 50 cm là:
40 + 16,7 = 56,7 %

Lá có đường kính từ 30 cm đến 50 cm có tân số là:
24+ 10= 34.
Do đó; tần suất của lá có đường kính từ 30 cm đến 50 cm là:
24 + 10 60 . 100 % = 56.7%
Chọn C.

\(X:1s^22s^22p^63s^23p^2\)
Vị trí: Nhóm VIA, chu kì 3


Để có tổng bằng 21,ta có thể làm như sau:
Ta rút :
C1: 10 và J *Vì hai lá này có giá trị là:10,11*
C2: 9 và Q *GIÁ trị 9 và 12*
C3: 8 và K *giá trị 8 và 13*
Vậy có tổng cộng 3 cách rút được 2 lá có tổng bằng 21.
sai sai ta