Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

Bài 1:
Để M có nghĩa thì \(\left\{{}\begin{matrix}x+4\ge0\\2-x\ge0\end{matrix}\right.\)
\(\Leftrightarrow\left\{{}\begin{matrix}x\ge-4\\x\le2\end{matrix}\right.\Leftrightarrow-4\le x\le2\)
Số giá trị nguyên thỏa mãn điều kiện là:
\(\left(2+4\right)+1=7\)

bài 5 nhé:
a) (a+1)2>=4a
<=>a2+2a+1>=4a
<=>a2-2a+1.>=0
<=>(a-1)2>=0 (luôn đúng)
vậy......
b) áp dụng bất dẳng thức cô si cho 2 số dương 1 và a ta có:
a+1>=\(2\sqrt{a}\)
tương tự ta có:
b+1>=\(2\sqrt{b}\)
c+1>=\(2\sqrt{c}\)
nhân vế với vế ta có:
(a+1)(b+1)(c+1)>=\(2\sqrt{a}.2\sqrt{b}.2\sqrt{c}\)
<=>(a+1)(b+1)(c+1)>=\(8\sqrt{abc}\)
<=>(a+)(b+1)(c+1)>=8 (vì abc=1)
vậy....

\(A=\frac{2}{\sqrt{5}-3}-\frac{2}{\sqrt{5}+3}=\frac{2\left(\sqrt{5}+3\right)-2\left(\sqrt{5}-3\right)}{-4}=\frac{2\sqrt{5}+6-2\sqrt{5}+6}{-4}=\frac{12}{-4}=-3\)
Vay ........

1.
A= \(2\sqrt{6}\) + \(6\sqrt{6}\) - \(8\sqrt{6}\)
A= 0
2.
A= \(12\sqrt{3}\) + \(5\sqrt{3}\) - \(12\sqrt{3}\)
A= 0
3.
A= \(3\sqrt{2}\) - \(10\sqrt{2}\) + \(6\sqrt{2}\)
A= -\(\sqrt{2}\)
4.
A= \(3\sqrt{2}\) + \(4\sqrt{2}\) - \(\sqrt{2}\)
A= \(6\sqrt{2}\)
5.
M= \(2\sqrt{5}\) - \(3\sqrt{5}\) + \(\sqrt{5}\)
M= 0
6.
A= 5 - \(3\sqrt{5}\) + \(3\sqrt{5}\)
A= 5
This literally took me a while, pls sub :D
https://www.youtube.com/channel/UC4U1nfBvbS9y_Uu0UjsAyqA/featured

\(a, x^3+5x^2-9x-45=0\\ \Leftrightarrow x^2\left(x+5\right)-9\left(x+5\right)=0\\ \Leftrightarrow\left(x-3\right)\left(x+3\right)\left(x+5\right)=0\\ \Leftrightarrow\left[{}\begin{matrix}x=3\\x=-3\end{matrix}\right.\left(x\ne-5\right)\\ \text{Với }x=3\Leftrightarrow A=\dfrac{9-9}{3\left(3+5\right)}=0\\ \text{Với }x=-3\Leftrightarrow A=\dfrac{9-9}{3\left(-3+5\right)}=0\\ \text{Vậy }A=0\\ b,B=\dfrac{x^2-3x+2x^2+6x-3x^2-9}{\left(x-3\right)\left(x+3\right)}\\ B=\dfrac{3x-9}{\left(x-3\right)\left(x+3\right)}=\dfrac{3\left(x-3\right)}{\left(x-3\right)\left(x+3\right)}=\dfrac{3}{x+3}\)

b: \(B=\dfrac{x^2-3x+2x^2+6x-3x^2-9}{x^2-9}=\dfrac{3x-9}{\left(x-3\right)\left(x+3\right)}=\dfrac{3}{x+3}\)
Ta có: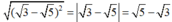
Đáp án: (C)