M
2
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Các câu hỏi dưới đây có thể giống với câu hỏi trên
NN
8 tháng 5 2020
Gọi chữ số hàng chục là x ( \(x\inℕ^∗\), \(4\le x\le9\))
Chữ số hàng đơn vị là: \(2x-7\)
Số tự nhiên ban đầu có dạng: \(10x+\left(2x-7\right)\)
Số tự nhiên ban đầu viết theo thứ tự ngược lại có dạng: \(10.\left(2x-7\right)+x\)
Nếu viết 2 chữ số ấy theo thứ tự ngược lại thì số mới nhỏ hơn số cũ 27 đơn vị nên ta có phương trình:
\(10.\left(2x-7\right)+x+27=10x+\left(2x-7\right)\)
\(\Leftrightarrow20x-70+x+27=10x+2x-7\)
\(\Leftrightarrow20x+x-10x-2x=-7+70-27\)
\(\Leftrightarrow9x=36\)\(\Leftrightarrow x=4\)( thoả mãn ĐK )
Vậy chữ số cần tìm là: \(41\)
9 tháng 2 2019
1. Gọi số bé và số lớn lần lượt là a và a + 1 \(\left(a\in Z\right)\)
Ta có: \(2a+3\left(a+1\right)=-87\)
\(\Leftrightarrow5a+3=-87\Leftrightarrow a=-18\Rightarrow a+1=-17\)
Vậy số lớn là -17 và số bé là -18
PT
0
9 tháng 8 2021
số lớn là x số nhỏ là y
\(\hept{\begin{cases}x=5y+22\left(1\right)\\8y=x+80\left(2\right)\end{cases}}\)thế pt 1 vào pt 2 ta được
\(8y=x+80\)
\(8y=5y+22+80\)
\(3y=102\)
\(y=34\)
\(< =>x=y.5+22\)
\(x=192\)
vậy số lớn là 192 số nhỏ là 34
\(\)
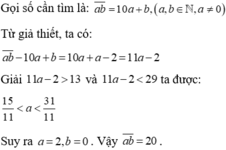
Lâu ko làm dạng này nên ko chắc đâu nha!
Gọi hai số tự nhiên đó là a, b (a>b).
Theo đề bài \(\hept{\begin{cases}\left(a;b\right)=4\left(1\right)\\b=8\left(2\right)\end{cases}}\)
Từ (1) suy ra: \(\hept{\begin{cases}a=4a_1\\b=4b_1\end{cases}}\text{với }\left(a_1;b_1\right)=1\)
Từ (2) suy ra \(b_1=2\) do đó \(\left(a_1;2\right)=1\)
Mà 2 là số nguyên tố \(\Rightarrow a_1⋮̸2\)\(\Rightarrow a_1\text{ là số lẻ}\Rightarrow a_1=2k+1\)
(k thuộc N*, do a1 > b1 ,vì a> b). Từ đó suy ra \(a=4a_1=4\left(2k+1\right)=8k+4\)
và b = 8.
Vậy....
P/s: Is it true??
Mình sai chỗ nào vại :<<