Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

Đáp án A.
Ta có:
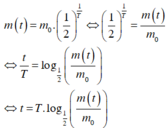
Theo giả thiết ta có:
T = 1602(năm), m 0 = 1 g r a m , m t = 0.5 g r a m
Áp dụng công thức ta có khoảng thời gian cần tìm là:
t = T . log 1 2 m t m 0 = 1602. log 1 2 0.5 1 = 1602. log 1 2 1 2 = 1602
Vậy sau 1602 năm thì 1gram chất phóng xạ này bị phân ra còn lại 0.5 gram

Gọi ∆ N 1 là số hạt β - được phóng ra trong khoảng thời gian ∆ t 1 kể từ thời điểm ban đầu.
Ta có
∆ N 1 = N 01 - N 1 = N 01 1 - e - k ∆ t 1
với N 01 là số hạt phóng xạ β - ban đầu.
Sau 3 giờ, số nguyên tử còn lại trong chất phóng xạ là N 02 = N 01 . e - 3 k .
Kể từ thời điểm này, trong khoảng thời gian ∆ t 2 thì số hạt β - tạo thành là
∆ N 2 = N 02 - N 01 = N 02 1 - e - k ∆ t 2
Cho ∆ t 1 = ∆ t 2 = 1 phút thì theo giả thiết, ta có ∆ N 1 = 960; ∆ N 2 = 120. Khi đó
∆ N 1 ∆ N 2 = e - 3 k ⇔ 120 960 = e - 3 k ⇔ 8 - 1 = e - 3 k ⇔ k = ln 2
Vậy T = k ln 2 = 1 (giờ) là chu kỳ bán rã của chất phóng xạ.
Đáp án B

Chọn A
Phương pháp:

Cách giải
Ban đầu, A = 100 con. Sau 5h có 300 con vi khuẩn


Giả sử tại thời điểm ban đầu mẫu đồ cổ có chứa khối lươgnj Cacbon là m o và tại thời điểm t (tính từ thời điểm ban đầu), khối lượng đó là m(t) thì ta có
m t = m o . e - ln 2 5730 ⇔ 75 % m o = m o - ln 2 5730 ⇔ t ≈ 2378
Đáp án C




Chọn C