Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

Đáp án A
Hàm số f(x) xác định trên D⊆ R
Điểm
x
0
∈ D được gọi là điểm cực đại của hàm số f(x) nếu tồn tại một khoảng (a;b)⊂ D sao cho
x
0
∈ (a;b) và f(
x
0
)>f(x),∀x ∈ (a,b)∖{
x
0
}.

Đáp án A
Hàm số f(x) xác định trên D⊆ R
Điểm xo∈ D được gọi là điểm cực đại của hàm số f(x) nếu tồn tại một khoảng (a;b)⊂ D sao cho xo∈ (a;b) và f(xo)>f(x),∀x ∈ (a,b)∖{xo}.

Ta có y ' = a cos x + b sin x + 1 .
Do hàm số đạt cực trị tại các điểm x = π 3 ; x = π nên
y ' π 3 = 0 y ' π = 0 ⇔ 1 2 a - 3 2 b + 1 = 0 - a + 1 = 0 ⇔ a = 1 b = 3
Do đó a + b 3 = 4
Đáp án C

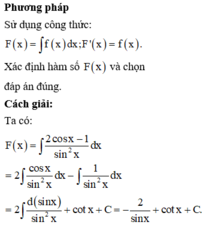
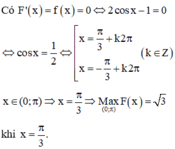
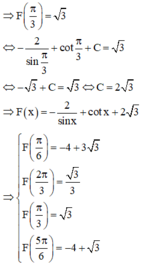
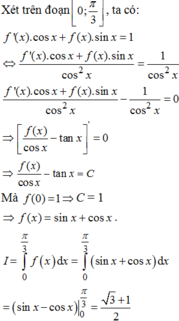

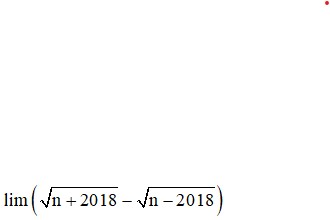
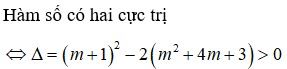
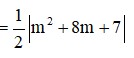
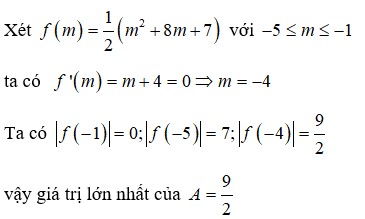

Đáp án là B.
Ta có y , = 2 a . cos 2 x - 2 b sin 2 x - 1 .Để hàm số đạt cực trị các điểm x = π 2 và x = π 2 thì y , ( π 6 ) = 0 y , ( π 2 ) = 0 ⇔ a - 3 b - 1 = 0 - 2 a - 1 = 0 ⇔ a = - 1 2 b = - 3 2 ⇒ a - b = 3 - 1 2