Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

Ta có:
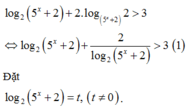
Ta có
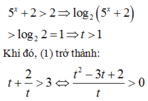
Ta có bảng xét dấu sau:
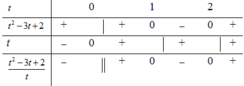
Từ BBT kết hợp điều kiện của t ta có:

Chọn: D

Đáp án A
log 2 5 x + 2 + 2 log 5 x + 2 2 > 3 ⇔ log 2 5 x + 2 + 2 log 2 5 x + 2 > 3 *
Đặt: t = log 2 5 x + 2 > 1 ,
Khi đó * ⇔ t + 2 t > 3 ⇔ t > 2
Khi đó:
log 2 5 x + 2 > 2 ⇔ 5 x > 2 ⇔ x > log 5 2 = log a b ⇒ a = 5 b = 2

Đáp án B.
Điều kiện: x ≢ 0 .
Phương trình 27 x - 1 x . 2 x = 72 ⇔ 3 3 x - 1 x . 2 x = 3 2 . 2 3 ⇔ 3 3 x - 3 x . 2 x - 3 = 1 ⇔ 3 x - 3 x . 2 x - 3 = 1
⇔ log 3 3 x - 3 x . 2 x - 3 = 0 ⇔ x - 3 x + x - 3 . log 3 2 = 0 ⇔ x - 3 + x x - 3 . log 3 2 = 0
⇔ x - 3 1 + x . log 3 2 = 0 ⇔ x = 3 x = - 1 log 3 2 = - log 2 3 → a = 2 , b = 3
Vậy a + b = 5 .

Chọn đáp án A
Ta có
![]()
![]()
Đặt t = 2 x > 0 thì phương trình đã cho trở thành t 2 - 2 m . t + m + 2 = 0 *
Để phương trình đã cho có hai nghiệm dương phân biệt khi và chỉ khi phương trình (*) có hai nghiệm t 1 , t 2 lớn hơn 1.
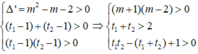
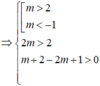
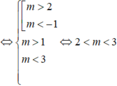
![]()

Đáp án A
Ta có 2 x . 15 x + 1 = 3 x + 3 ⇔ 2 x . 5 x + 1 = 3 2 ⇔ log 2 x . 5 x + 1 = log 3 2 ⇔ x log 2 + x + 1 log 5 = 2 log 3
⇔ x log 2 + log 5 = 2 log 3 - log 5 ⇔ x = 2 log 3 - log 5 log 2 + log 5 = 2 log 3 - log 5 ⇒ a = 3 b = 5 .
Vậy S = 4009.
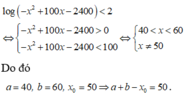
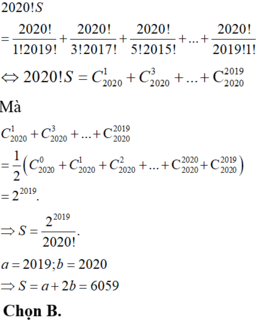

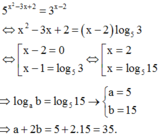
Đáp án C