Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

Chọn C.
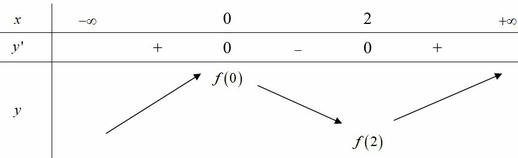
Dựa vào đồ thị hàm số f ' ( x ) suy ra BBT của hàm số y = f(x)

Khẳng định 1, 2, 5 đúng, khẳng định 4 sai.
Xét khẳng định 3: Ta có:
f ( 3 ) + f ( 2 ) = f ( 0 ) + f ( 1 ) ⇒ f ( 3 ) - f ( 0 ) = f ( 1 ) - f ( 2 ) > 0
Do đó f ( 3 ) > f ( 0 ) ⇒ Vậy khẳng định 3 đúng.

Đáp án C
Ta có f ' x = 0 ⇔ x = 1 ; 2 ; 3 ⇒ hàm số có 3 điểm cực trị
Lại có g x = f x - m - 2018 ⇒ g ' x = f ' x = 0 ⇒ có 3 nghiệm phân biệt
Suy ra phương trình f x = m + 2018 có nhiều nhất 4 nghiệm
Xét y = f x + 1 ⇒ y ' = f ' x + 1 < 0 ⇔ [ x + 1 ∈ 1 ; 2 x + 1 ∈ 3 ; + ∞ ⇔ [ 0 < x < 1 x > 2
Suy ra hàm số y = f(x + 1) nghịch biến trên khoảng (0;1).

Đáp án B
Phương pháp: Từ đồ thị hàm số y = f’(x) lập BBT của đồ thị hàm số y = f(x) và kết luận.
Cách giải: Ta có 
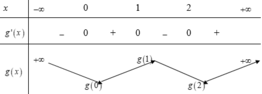
BBT:
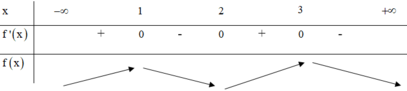
Từ BBT ta thấy (I) đúng, (II) sai.
Với ![]() => Hàm số y = f(x+1) nghịch biến trên khoảng (0;1).
=> Hàm số y = f(x+1) nghịch biến trên khoảng (0;1).
=>(III) đúng.
Vậy có hai khẳng định đúng








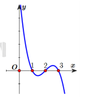 Xét các khẳng định sau:
Xét các khẳng định sau: 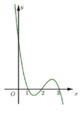
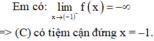

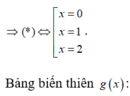
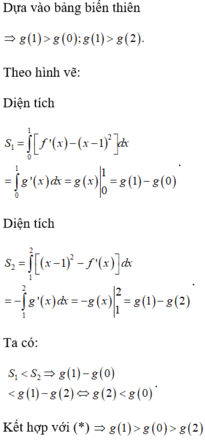
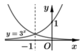
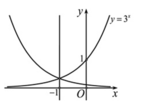
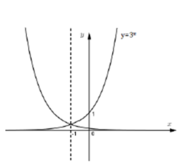
Gọi M(x;y) và M'(x';y') là hai điểm đối xứng nhau qua đường thẳng x = -1 nên
Trắc nghiệm: Chọn
A'(-2;1) chỉ có đáp án B thỏa.