
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.


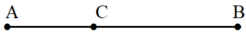
Vì điểm C nằm giữa hai điểm A và B nên ta có: AC + CB = AB
+ Với AB = 10; BC = 3 ta có AC + CB = AB nên AC = AB − BC = 10 − 3 = 7
+ Với AB = 12; AC = 5 ta có AC + CB = AB nên BC = AB − AC = 12 − 5 = 7
+ Với BC = 7; AC = 8 ta có AC + CB = AB hay AB = 8 + 7 = 15.
Ta có bảng sau:
| AB | BC | AC |
| 10 | 3 | 7 |
| 12 | 7 | 5 |
| 15 | 7 | 8 |

AB = 0 còn nói là (4) khoảng cách giữa hai điểm A và B bằng (2) 0 hoặc hai điểm A và B (1) trùng nhau hoặc (3) độ dài đoạn thẳng AB bằng (2) 0 hoặc A (5) cách B một khoảng bằng (2) 0.

A) Nếu M nằm giữa A và B thì AM+MB=AB
B) Trong 3 điểm thẳng hàng thì có 1 điểm nằm giữa 2 điểm còn lại
C) Mỗi điểm trên đường thẳng là gốc trung của 2 tia đối nhau

Hai điểm A và B trùng nhau còn nói là (4) khoảng cách giữa hai điểm A và B bằng (2) 0 hoặc A (5) cách B một khoảng bằng (2) 0 hoặc (3) độ dài đoạn thẳng AB bằng (2) 0.


Chọn (B) 5cm.
Vì E là trung điểm đoạn MN nên EN = MN : 2 = 3 : 2 = 1,5cm.
Vì F là trung điểm đoạn NP nên NF = NP : 2 = 7 : 2 = 3,5cm.
Vì N nằm giữa M và P nên hai tia NM và NP đối nhau. (1)
Lại có E là trung điểm đoạn MN nên E thuộc tia NM; F là trung điểm đoạn NP nên F thuộc tia NP
Kết hợp với (1) ta suy ra N là điểm nằm giữa E và F.
Do đó EF = EN + NF = 1,5 + 3,5 = 5cm
Vậy EF = 5cm.

C nằm giữa A và B => AC + BC = AB
D là trung điểm của AC => CD = AC/2
E là trung điểm của BC => CE = BC/2
Vì \(D\in AC;E\in BC\) => C nằm giữa D và E
=> DE = DC + CE = AC/2 + BC/2 = (AC + BC)/2 = AB/2
Vậy DE = a/2
ta có \(DE=DC+CE=\frac{AC}{2}+\frac{CB}{2}=\frac{AC+CB}{2}=\frac{AB}{2}=\frac{a}{2}\left(cm\right)\)

AB = 2 (cm) còn nói là (4) khoảng cách giữa hai điểm A và B bằng 2 (cm) hoặc nói là (3) độ dài đoạn thẳng AB bằng 2 (cm) hoặc A (5) cách B một khoảng bằng 2 (cm).

Theo giả thiết ta vẽ được hình:

Khi đó AN = AM + MN và AB = AN + NB.
Suy ra AB = (AM + MN) + NB
Do AM = NB = 2 cm nên 10 = 2 + MN + 2.
Từ đó tính được MN = 10 - 4 = 6 (cm)