
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.


|
Xét tổng
Suy ra có ít nhất một trong 7 số |
![]()
![]() là số chẵn
là số chẵn

Với a = -7 và b = 4. Ta có:
a2+2.a.b + b2 = (-7)2+ 2.(-7).4 + 42 = 49 – 56 + 16 = 9
(a + b). (a + b) = [(-7) + 4].[(-7) + 4] = (-3).(-3) = 9

Bài 1:
ta có:\(\hept{\begin{cases}a.b=18\\a+b=11\end{cases}}\)
pt (1) \(\Leftrightarrow b\left(11-b\right)=18\)
\(\Rightarrow11b-b^2=18\)
\(\Rightarrow-\left(11b+b^2\right)=18\)
\(\Rightarrow b^2+11b=18\)
\(\Rightarrow b^2+11b+18=0\)
\(\Rightarrow b^2+11b+22-4=0\)
\(\Rightarrow\left(b+11\right)-4=0\)
\(\Rightarrow\left(b+11+2\right).\left(b+11-2\right)=0\)
\(\Rightarrow\left(b+13\right).\left(b+9\right)=0\)
\(\Rightarrow\hept{\begin{cases}b=-13\Leftrightarrow a=2\\b=-9\Leftrightarrow a=-2\end{cases}}\)
Bài 2:
2)
P=-[(2x-6)2+/-5-y/-37]
Vi (2x-6)2 ≥0 , /-5-y/≥0 nên (2x-6)2+/-5-y/-37-37/ => P≤37
Dấu = xảu ra khi x=3 , y=-5
Vậy Max P=37 khi x=3 , y=-5
chúc bạn học tốt !

a, a(b+c)−b(a−c)a(b+c)−b(a−c)
=ab+ac−(ab−bc)=ab+ac−(ab−bc)
=ab+ac−ab+bc=ab+ac−ab+bc
=ac+bc=ac+bc
=(a+b)c=(a+b)c
b,(a+b)(a−b)(a+b)(a−b)
=(aa+ab)−(ab+bb)=(aa+ab)−(ab+bb)
=aa+ab−ab−bb

Kí hiệu D là tập hợp các con đường đi từ A tới C qua B
D = {a1b1; a2b1; a1b2; a2b2; a1b3; a2b3}

vậy thì tôi đoán ko lầm thì a=3, b=900 hoặc a=900 và b=3

Lập bảng:
| a + 1 | -3 | -1 | 1 | 3 |
| a | -4 | -2 | 0 | 2 |
| b + 2 | -1 | -3 | 3 | 1 |
| b | -3 | -5 | 1 | -1 |
Vậy cặp (a; b) lớn nhất là: (0; 1)
(a+1)(b+2)=3
đề thỏa mãn a.b lớn nhất thì a và b lớn nhất=>(a+1)(b+2) cũng phải lớn nhất
3=1.3=3.1=(-1).(-3)=(-3).(-1)
để lớn nhất thì (a+1)(b+1)=3.1(hoặc 1.3)
a+1=3=>a=2
b+1=1=>b=0
=>a.b=0(lớn nhất)

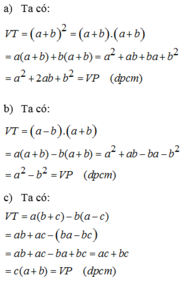
ta giả sử \(\left(a^2+b^2,a.b\right)=k\) với k là số tự nhiên khác 1.
do đó a.b chia hết cho k , mà (a,b)=1 nên hoặc a chia hết cho k, hoặc b chia hết cho k
với a chia hết cho k thì a2 cũng chia hết cho k, mà a2+b2 cũng chia hết cho k
Nên b2 chia hết cho k. nên b chia hết cho k.
vì vậy (a,b) phải chia hết cho k
điều này mâu thuẫn với giả sử nên ta có điều phải chứng minh
hoàn toàn tương tự cho khả năng b chia hết cho k.