Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

a) Tứ giác ABCD là hình bình hành => AB//CD
mà AK=1/2AB(gt)
IC=1/2DC(gt)
nên tứ giác ABCD là hình bình hành (tứ giác có một cặp cạnh đối vừa song song vừa bằng nhau).
Do đó AI // CK(hai cạnh đối của hình bình hành)
b) ∆DCN có DI = IC(gt)
IM // CN(IA//KC,M thuộc AI,N thuộc KC)
vậy M là trung điểm của DN=>DM = MN(1)
Xét ∆ABM ta có AK=KB(gt)
NK//MK(AI//KC,M thuộc AI,N thuộc KC) => N là trung điểm của MB=> NM=NB (2)
từ (1)+(2)=> DM = MN = NB

Bài 16. Giải thích vì sao diện tích của tam giác được tô đậm trong các hình 128,129, 130 bằng nửa diện tích hình chữ nhật tương ứng:
Hướng dẫn giải:
Ở mỗi hình 128, 129, 130; hình tam giác và hình chữ nhật đều có cùng đáy a và cùng chiều cao h nên diện tích của tam giác bằng nửa diện tích hình chữ nhật tương ứng.
tk nha bạn
thank you bạn

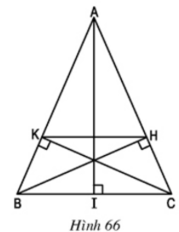
a) Xét hai Δvuông HBC và ΔKCB
∠BCH = ∠CBK (Δ ABC cân tại A) BC cạnh chung
⇒ ΔHBC = ΔKCB (cạnh huyền, góc nhọn)
⇒ CH = BK
b) Ta có: AB = AC (ΔABC cân tại A) và CH = BK
- Quảng cáo -
AK = AB – BK và AH = AC – CH ⇒ AK = AH
⇒ AK/AB = AH/AC ⇒ KH//BC
c) Kẻ đường cao AI của Δ ABC và xét Δ IAC
ΔHBC có ∠ACI = ∠BCH
⇒ ΔIAC ∽ ΔHBC(g.g) ⇒ AC/BC = IC/HC ⇒ HC = IC.BC / AC = a2/2b
Ta có : \(KH//BC\Rightarrow\frac{KH}{BC}=\frac{AH}{AC}\)
\(\Rightarrow KH=\frac{AH.BC}{AC}=\frac{\left(AC-HC\right).BC}{AC}\)
\(\Rightarrow KH=\left(b-\frac{a^2}{2b}\right)\frac{a}{b}=a-\frac{a^3}{2b^2}\)

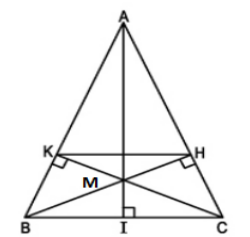
Ta có MD // AE (vì MD // AB)
ME //AD (vì ME // AC)
Nên AEMD là hình bình hành, I là trung điểm của DE nên I cũng là trung điểm của AM, do đó A đối xứng với M qua I
GT: Cho hình 82, trong đó MD // AB, ME // AC
KL: Chứng minh A đối xứng với M qua I
GIẢI:
Ta có: MD // AE (vì MD // AB)
ME // AD (vì ME // AC)
Nên AEMD là hình bình hành, I là trung điểm của DE nên I cũng là trung điểm của AM, do đó A đối xứng với M qua I

a) Tứ giác ABCD có AB = CD, AD = BC nên là hình bình hành.
Tứ giác AICK có AK // IC, AK = IC nên là hình bình hành.
Do đó AI // CK
b) ∆DCN có DI = IC, IM // CN.
(vì AI // CK) nên suy ra DM = MN
Chứng minh tương tự đối với ∆ABM ta có MN = NB.
Vậy DM = MN = NB