
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.


Toán 7 ( Đại sô )
Bài 2: SGK/7

Vậy những phân số biểu diễn số hữu tỉ 3/-4 là: -15/20; 24/-32; -27/36
Bài 3: SGK/8
a) x= 2/-7 = -22/7;y = -3/11= -21/77
Vì -22 < -21 và 77> 0 nên x <y
b)![]() Vì -216 < -213 và 300 > 0 nên y < x
Vì -216 < -213 và 300 > 0 nên y < x
c) x = -0,75 = -75/100 = -3/4; y = -3/4
Vậy x=y
Bài 4: SGK/8
Với a, b ∈ Z, b> 0
– Khi a , b cùng dấu thì a/b > 0
– Khi a,b khác dấu thì a/b < 0
Tổng quát: Số hữu tỉ a/b ( a,b ∈ Z, b # 0) dương nếu a,b cùng dấu, âm nếu a, b khác dấu, bằng 0 nếu a = 0
Bài 5: SGK/8
Theo đề bài ta có ( a, b, m ∈ Z, m > 0)
( a, b, m ∈ Z, m > 0)
Vì x < y nên ta suy ra a< b
Ta có :
Vì a < b ⇒ a + a < a +b ⇒ 2a < a + b
Do 2a< a +b nên x < z (1)
Vì a < b ⇒ a + b < b + b ⇒ a + b < 2b
Do a+b < 2b nên z < y (2)
Từ (1) và (2) ta suy ra x < z< y

A=1+3/2^3+4/2^4+5/2^5+...100/2^100
1/2*A = 1/2 + 3/2^4 + 4/2^5 +....+ 99/2^100 + 100/2^101
A- A/2 = 1/2A =1/2 + 3/2^3 + 1/2^4 +...+1/2^100 - 100/2^101
= [1/2+1/2^2 +1/2^3 +...+1/2^100] -100/2^101 (Do 3/2^3 = 1/2^2 +1/2^3)
=[1-(1/2)^101]/(1-1/2) -100/2^101
=(2^101 -1)/2^100 - 100/2^101
=> A = (2^101 -1)/2^99 - 100/2^100
Bạn ơi khó hiểu quá bạn giải chi tiết hơn giúp mình nhé mình sẽ k cho bạn 2 cái nhé

3n + 3 + 3n + 1 + 2n + 3 + 2n + 2
= 3n.33 + 3n.3 + 2n.23 + 2n.22
= 3n.(27 + 3) + 2n.(8 + 4)
= 3n.30 + 2n.12
= 3n.5.6 + 2n.2.6
= 6.(3n.5 + 2n.2) \(⋮\) 6

Ta có: \(6-\left(x-\dfrac{1}{3}\right)^2=2^{2021}:\left(-2\right)^{2020}\)
\(\Leftrightarrow6-\left(x-\dfrac{1}{3}\right)^2=2^{2021}:2^{2020}\\ \Leftrightarrow6-\left(x-\dfrac{1}{3}\right)^2=2\\ \Leftrightarrow\left(x-\dfrac{1}{3}\right)^2=4\\ \Rightarrow\left[{}\begin{matrix}x-\dfrac{1}{3}=2\\x-\dfrac{1}{3}=-2\end{matrix}\right.\\ \Rightarrow\left[{}\begin{matrix}x=\dfrac{7}{3}\\x=-\dfrac{5}{3}\end{matrix}\right.\)
Vậy \(\left[{}\begin{matrix}x=\dfrac{7}{3}\\x=-\dfrac{5}{3}\end{matrix}\right.\)

Câu 1.
\(M=\left(-\dfrac{2a^3b^2}{3}xy^2z\right)^3.\left(-\dfrac{3}{4}ab^{-3}x^2yz^2\right)^2.\left(-xy^2z^2\right)^2\)
\(=\left(-\dfrac{8}{27}a^9b^6x^3y^6z^3\right).\left(\dfrac{9}{16}a^2b^{-6}x^4y^2z^4\right).\left(x^2y^4z^4\right)\)
\(=-\dfrac{8}{27}.\dfrac{9}{16}.a^{11}x^9y^{12}z^{11}\)
\(=-\dfrac{1}{6}a^{11}x^9y^{12}z^{11}\)
Hệ số: \(-\dfrac{1}{6}\)
Bậc: \(43\)
Câu 2.
a) \(A\left(x\right)=\dfrac{1}{2}x^5+\dfrac{3}{4}x-12x^4-1\dfrac{2}{3}x^3+5+x^2+\dfrac{5}{3}x^3-\dfrac{11}{4}x+1\dfrac{1}{2}x^5+4x\)
\(=\left(\dfrac{1}{2}x^5+\dfrac{3}{2}x^5\right)+\left(-12x^4\right)+\left(-\dfrac{5}{3}x^3+\dfrac{5}{3}x^3\right)+x^2+\left(\dfrac{3}{4}x-\dfrac{11}{4}x+4x\right)+5\)
\(=2x^5-12x^4+x^2+2x+5\)
\(B\left(x\right)=-2x^5+\dfrac{3}{7}x+12x^4-\dfrac{7}{3}x^3-3-6x^2+\dfrac{13}{3}x^3+3\dfrac{4}{7}x\)
\(=\left(-2x^5\right)+12x^4+\left(-\dfrac{7}{3}x^3+\dfrac{13}{3}x^3\right)-6x^2+\left(\dfrac{3}{7}x+\dfrac{25}{7}x\right)-3\)
\(=-2x^5+12x^4+2x^3-6x^2+4x-3\)
b) \(C\left(x\right)=A\left(x\right)+B\left(x\right)=\left(2x^5-12x^4+x^2+2x+5\right)+\left(-2x^5+12x^4+2x^3-6x^2+4x-3\right)\)
\(=\left(2x^5-2x^5\right)+\left(-12x^4+12x^4\right)+2x^3+\left(x^2-6x^2\right)+\left(2x+4x\right)+\left(5-3\right)\)
\(=2x^3-5x^2+6x+2\)
\(D\left(x\right)=A\left(x\right)-B\left(x\right)=\left(2x^5-12x^4+x^2+2x+5\right)-\left(-2x^5+12x^4+2x^3-6x^2+4x-3\right)\)
\(=\left(2x^5+2x^5\right)+\left(-12x^4-12x^4\right)-2x^3+\left(x^2+6x^2\right)+\left(2x-4x\right)+\left(5+3\right)\)
\(=4x^5-24x^4-2x^3+7x^2-2x+8\)
c) \(2x^3-5x^2+6x+2-2x^3+5x^2=-4\)
\(\Rightarrow\left(2x^3-2x^3\right)+\left(-5x^2+5x^2\right)+6x+2\)
\(\Rightarrow6x+2=-4\)
\(\Rightarrow6x=-6\)
\(\Rightarrow x=-1\)
Câu 3.
1) \(M-3xy^2+2xy-x^3+2x^2y=2xy-3x^3+3x^2y-xy^2\)
\(\Rightarrow M=\left(3xy^2+2xy-x^3+2x^2y\right)+\left(2xy-3x^3+3x^2y-xy^2\right)\)
\(=\left(3xy^2-xy^2\right)+\left(2xy+2xy\right)+\left(-x^3-3x^3\right)+\left(2x^2y+3x^2y\right)\)
\(=2xy^2+4xy-4x^3+5x^2y\)
2)
Để cho \(f\left(x\right)\) có nghiệm thì \(6-3x=0\)
\(\Rightarrow3x=6\)
\(\Rightarrow x=2\)
Để cho \(g\left(x\right)\) có nghiệm thì \(x^2-1=0\)
\(\Rightarrow x^2=1\)
\(\Rightarrow\left[{}\begin{matrix}x=1\\x=-1\end{matrix}\right.\)
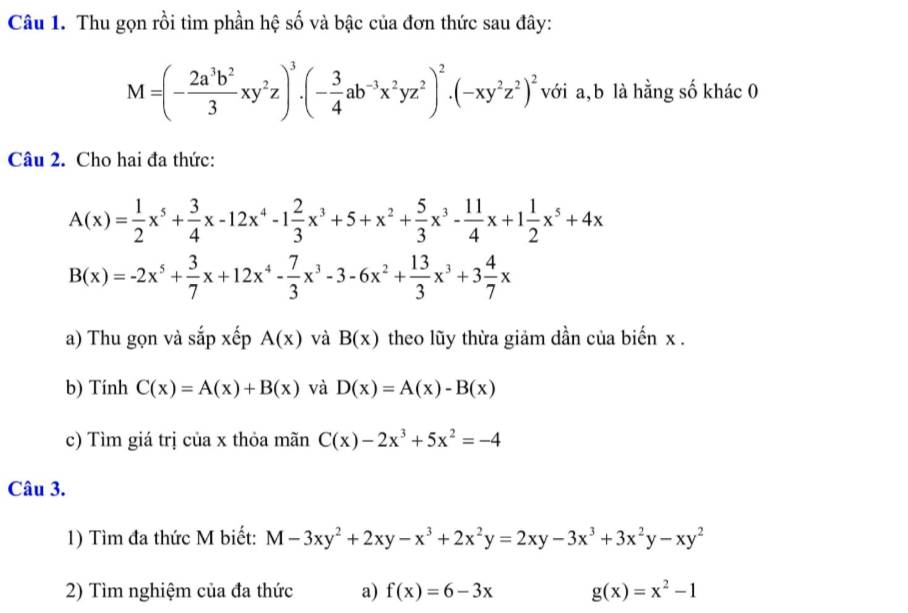

Cộng trừ hai số hữu tỉ
B6:
a, \(\frac{-1}{21}+\frac{-1}{28}\) = \(\frac{-1}{12}\)
\(b,\frac{-8}{18}-\frac{15}{27}\) = -1
\(c,\frac{-5}{12}+0,75=\frac{1}{3}\)
\(d,3,5-\left(\frac{-2}{7}\right)=\frac{53}{14}\)
\(B8:\)
\(a,\frac{3}{7}+\left(\frac{-5}{2}\right)+\left(\frac{-3}{5}\right)\)
= \(\frac{3}{7}-\frac{5}{2}-\frac{3}{5}\)
\(=\frac{-187}{70}\)
\(b,\left(\frac{-4}{3}\right)+\left(\frac{-2}{5}\right)+\left(\frac{-3}{2}\right)\)
\(=\frac{-4}{3}-\frac{2}{5}-\frac{3}{2}\)
\(=\frac{-97}{30}\)
\(c,\frac{4}{5}-\left(\frac{2}{7}\right)-\frac{7}{10}\)
\(=\frac{4}{5}+\frac{2}{7}-\frac{7}{10}\)
\(=\left(\frac{4}{5}-\frac{7}{1}\right)+\frac{2}{7}\)
\(=\frac{1}{10}+\frac{2}{7}\)
\(=\frac{27}{70}\)
\(d,\frac{2}{3}-\left[\left(\frac{-7}{4}\right)-\left(\frac{1}{2}+\frac{3}{8}\right)\right]\)
\(=\frac{2}{3}-\left(\frac{-7}{4}-\frac{7}{8}\right)\)
\(=\frac{2}{3}-\left(\frac{-21}{8}\right)\)
\(=\frac{79}{24}\)
Làm từng bài một nha
Chẳng biết đúng hay sai nữa
bài phải nói rõ hơn chứ