Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

gọi 4 số cần tìm lần lượt là a,b,c,d
theo đề ta có;
\(\frac{\left(a+b+c+d\right)}{4}=45\) (1)
a-2=b:2=c+2=2d
ta đặt: a-2=b:2=c+2=2d=k
suy ra a=k+2;b=2k;c=k-2;d=k:2 (2)
thay (2) vào (1), ta được:
\(\frac{\left(a+b+c+d\right)}{4}=45\)
\(\frac{\left(k+2+2k+k-2+\frac{k}{2}\right)}{4}=45\)
\(\frac{9}{2}k=180\)
\(k=40\)
\(\Rightarrow a=k+2=40+2=42\)
\(\Rightarrow b=2k=2.40=80\)
\(\Rightarrow c=k-2=40-2=38\)
\(\Rightarrow d=\frac{k}{2}=\frac{40}{2}=20\)

Tập S có tất cả 2 6 = 64 tập con. Mỗi bạn có 64 cách viết ngẫu nhiên. Nên số phần tử không gian mẫu bằng 64 3
Ta tìm số cách viết thoả mãn:
Gọi x, y, z là số phần tử có trong các tập con của A, B, C viết lên bảng.
Vì các tập con của ba bạn này viết khác rỗng nên x , y , z ≥ 1
Vì các tập con của ba bạn này đôi một không giao nhau và trên bảng có đúng 4 phần tử của S nên x+y+z=4
Vậy ta có hệ 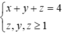
⇔ ( x ; y ; z ) = 1 ; 1 ; 2 ; 1 ; 2 ; 1 ; 2 ; 1 ; 1
Vậy có tất cả ![]() cách viết thoả mãn.
cách viết thoả mãn.
Xác suất cần tính bằng ![]()
Chọn đáp án B.

Đáp án A
n Ω = A 6 4 = 360 Xét x , y , z , t ∈ 1 ; 2 ; 3 ; 4 ; 5 ; 6 và x + y + z + t = 10
Giả sử
x < y < z < t ⇒ 4 x < 10 ⇒ x < 5 2 ⇒ x ≤ 2
và
y ≥ x + 1, z ≥ x + 2, t ≥ x + 3
Ta chọn được x = 1, y = 2, z = 3, t = 4 nên số hoán vị của 4 phần tử 4 ! loại đi 1234 còn lại 4 ! − 1 = 23 dãy. Vậy P = 23 360

Với 3 số 3, cách làm rất đơn giản: 3 x 3 - 3 = 6.
Sử dụng phép 6 + 6 - 6 = 6 đối với 3 số 6.
Đối với 3 số 4, ta có thể sử dụng phép căn bậc hai từng số rồi tính tổng của chúng.
Với 3 số 9, ta sử dụng phép căn bậc hai của 9 thành 3 rồi tính như trong trường hợp 3 số 3.
Cách làm đối với 3 số 5 và 3 số 7 tương tự nhau:
5 + 5 : 5 = 6
7 - 7 : 7 = 6
3 số 8 là trường hợp dễ gây nhầm lẫn nhất vì nhiều người sẽ sử dụng phép căn bậc ba của 8 bằng 2 rồi tính tổng của chúng. Tuy nhiên, người ra đề quy định, người giải không được thêm bất kỳ số tự nhiên nào trong khi ký hiệu căn bậc ba có số 3.
Trong trường hợp này, Ty Yann dùng hai lần căn bậc hai của 8 + 8 (tương đương căn bậc 4 của 16) bằng 2. Sau đó, ông dùng phép tính 8 - 2 = 6.
Với 3 số 1, tác giả dùng phép giai thừa:
(1 + 1 + 1)! = 3! = 3 x 2 x 1 = 6.

Số bị trừ = hiệu cộng với số trừ
Vậy ta có :
Số bị trừ cộng với số trừ= 1998
Số bị trừ là: 1998:2=999
Số trừ là:(999-135):2=432
ĐS: số trừ :432
SBT + ST + H = 1998
( ST + H ) + ST + H = 1998
=> 2 lần số trừ = số bị trừ
Vậy số bị trừ là :
1998 : 2 = 999
Số bị trừ bằng 999 hay tổng của số trừ và hiệu cũng bằng 999
Số trừ là :
( 999 - 135 ) : 2 = 432
Đáp số : 432

Chọn đáp án A.
Số phần tử của không gian mẫu là ![]()
Tích ba số không chia hết cho 3 khi và chỉ khi cả ba số đó đều không chia hết cho 3. Các thẻ được viết số không chia hết cho 3 bao gồm 7 thẻ mang số 1; 2; 4; 5; 7; 8; 10. Số cách lấy được 3 thẻ mà tích ba số viết trên ba thẻ không chia hết cho 3 là C 7 3 = 35
Suy ra, số cách lấy được 3 thẻ mà tích ba số viết trên ba thẻ chia hết cho 3 là ![]()
![]()
Ta có:
\(119+58-117=60\)
61-2+1=60