Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

Đáp án A
Thời điểm t số hạt nhân mẹ và hạt nhận con được tính bởi
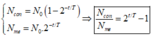
*Hạt nhân X là hạt nhân mẹ ở thời điểm t. Hạt nhân Y là hạt nhân con ở thời điểm t
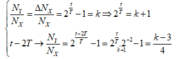

X --> Y
Tại thời điểm t1, giả sử có 1 X thì có k Y
Tại thời điểm t2 (sau 3 chu kì), X còn lại là \(\dfrac{1}{2^3}=\dfrac{1}{8}\), Y tạo thêm (do X phân rã) là: \(1-\dfrac{1}{8}=\dfrac{7}{8}\)
Như vậy, tỉ lệ lúc này giữa Y và X là: \(\dfrac{k+\dfrac{7}{8}}{\dfrac{1}{8}}=8k+7\)
Chọn D

Gọi số hạt nhân X ban đầu là N 0 , tại thời điểm t 1 số hạt nhân X còn lại là N x , số hạt nhân Y tạo thành là : N Y = N 0 - N X
Tỉ lệ 4 N X = 3 N Y
+ Tại thời điểm t 2 số hạt nhân X còn lại là N X X , số hạt nhân Y tạo thành là N YY = N x - N XX

Đáp án D

Sau thời gian t1 số hạt nhân còn lại là
\(N = N_0 2^{-\frac{t}{T}}\)=> \(\frac{N}{N_0}= 0,2= 2^{-\frac{t_1}{T}}=> t_1 = -T.\ln_20,2.\)
Sau thời điểm t2 thì số hạt nhân còn lại là
\(N_1 = N_0 2^{-\frac{t_2}{T}}=> \frac{N}{N_0} = 0,05 = 2^{-\frac{t_2}{T}}\)=> \(t_2 = -T\ln_20,05.\)
Mà \(t_2 = t_1 +100\)
=> \(-T \ln_2 0,05 = -T\ln_2 0,2 + 100\)
=> \(T = \frac{100}{\ln_2{(0,2/0,05)}}=50 s. \)
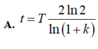
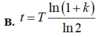
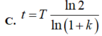
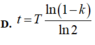
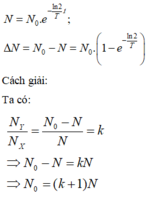
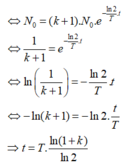
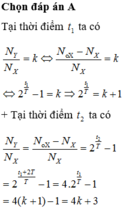
Đáp ánA