
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.



\(\dfrac{1100}{x}-\dfrac{1100}{x+5}=2\)
\(\Leftrightarrow\dfrac{1105-1100}{x+5}=2\)
\(\Leftrightarrow\dfrac{5}{x-5}=2\)
\(\Leftrightarrow5=2\left(x-5\right)\)
\(\Leftrightarrow5=2x-10\)
\(\Leftrightarrow2x=15\)
\(\Leftrightarrow x=\dfrac{15}{2}=7,5\)
\(\dfrac{1100}{x}-\dfrac{1100}{x+5}=2\left(ĐK:x\ne0;x\ne-5\right)\\ \Leftrightarrow\dfrac{1100\left(x+5\right)-1100x}{x\left(x+5\right)}=\dfrac{2x\left(x+5\right)}{x\left(x+5\right)}\\ \Leftrightarrow2x^2+10x-5500=0\\ \Leftrightarrow2x^2-100x+110x-5500=0\\ \Leftrightarrow2x.\left(x-50\right)+110.\left(x-50\right)=0\\ \Leftrightarrow\left(2x+110\right).\left(x-50\right)=0\\ \Leftrightarrow\left[{}\begin{matrix}2x+110=0\\x-50=0\end{matrix}\right.\\ \Leftrightarrow\left[{}\begin{matrix}x=-55\left(TM\right)\\x=50\left(TM\right)\end{matrix}\right.\)
Vậy: S={-55;50}

\(\sqrt{6+2\sqrt{5}}+\sqrt{6-2\sqrt{5}}=\sqrt{\left(\sqrt{5}+1\right)^2}+\sqrt{\left(\sqrt{5}-1\right)^2}\)
\(=\sqrt{5}+1+\sqrt{5}-1=2\sqrt{5}\)
\(\sqrt{11+6\sqrt{2}}-\sqrt{11-6\sqrt{2}}=\sqrt{\left(3+\sqrt{2}\right)^2}-\sqrt{\left(3-\sqrt{2}\right)^2}\)
\(=\left(3+\sqrt{2}\right)-\left(3-\sqrt{2}\right)=2\sqrt{2}\)
\(\sqrt{a^2+6a+9}+\sqrt{a^2-6a+9}=\sqrt{\left(a+3\right)^2}+\sqrt{\left(3-a\right)^2}\)
\(=\left|a+3\right|+\left|3-a\right|=3+a+3-a=6\)

Bài 2:
a: \(\dfrac{\sqrt{5}}{\sqrt{3}}=\dfrac{\sqrt{15}}{3}\)
b: \(\dfrac{13}{5-\sqrt{3}}=\dfrac{65+13\sqrt{3}}{22}\)
c: \(\dfrac{2\sqrt{2}}{\sqrt{7}+\sqrt{3}}=\dfrac{2\sqrt{14}-2\sqrt{6}}{4}=\dfrac{\sqrt{14}-\sqrt{6}}{2}\)
d: \(\dfrac{5-\sqrt{3}}{\sqrt{6}-2\sqrt{2}}=\dfrac{-3\sqrt{6}-7\sqrt{2}}{2}\)
Bài 3:
a: \(\dfrac{2}{\sqrt{3}-1}-\dfrac{2}{\sqrt{3}+1}\)
\(=\sqrt{3}+1-\sqrt{3}+1\)
=2
b: \(\dfrac{1}{3-\sqrt{3}}+\dfrac{1}{3+\sqrt{2}}\)
\(=\dfrac{3+\sqrt{3}}{6}+\dfrac{3-\sqrt{2}}{7}\)
\(=\dfrac{21+7\sqrt{3}+18-6\sqrt{2}}{42}\)
\(=\dfrac{39+7\sqrt{3}-6\sqrt{2}}{42}\)

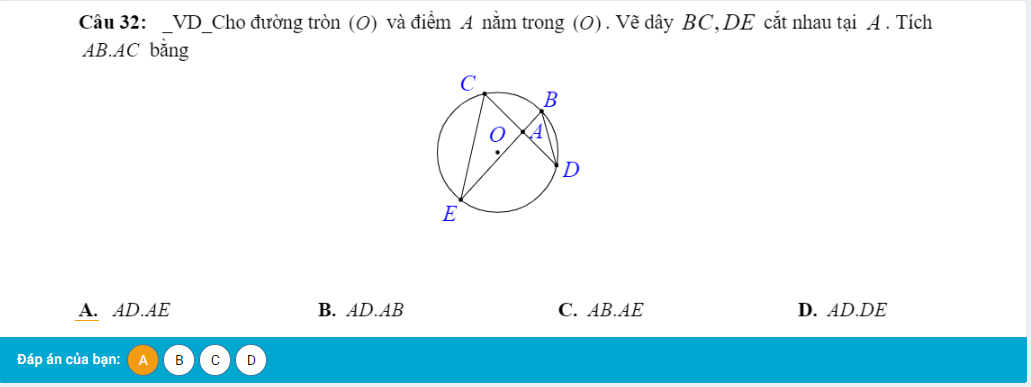
Xét (O) có
MA là tiếp tuyến có A là tiếp điểm
MB là tiếp tuyến có B là tiếp điểm
Do đó: MA=MB
Xét (O) có
NA là tiếp tuyến có A là tiếp điểm
NC là tiếp tuyến có C là tiếp điểm
Do đó: NA=NC
Ta có: MN=NA+MA
nên MN=MB+NC

Bài 3:
a: Ta có: \(A=3\sqrt{3}+5\sqrt{12}-2\sqrt{27}\)
\(=3\sqrt{3}+10\sqrt{3}-6\sqrt{3}\)
\(=7\sqrt{3}\)
b: ta có: \(B=\left(\sqrt{20}-\sqrt{45}+3\sqrt{5}\right):\sqrt{5}\)
\(=\left(2\sqrt{5}-3\sqrt{5}+3\sqrt{5}\right):\sqrt{5}\)
=2
c: ta có: \(C=\sqrt{5-\sqrt{13+\sqrt{48}}}\)
\(=\sqrt{5-2\sqrt{3}-1}\)
\(=\sqrt{3}-1\)

`(-2m+4)/(3m-2)=5/2`
`<=>2(-2m+4)=5(3m-2)`
`<=>-4m+8=15m-10`
`<=>18=19m`
`<=>m=18/19`

\(a,B=\dfrac{2\sqrt{x}+x-x-\sqrt{x}-1}{\left(\sqrt{x}-1\right)\left(x+\sqrt{x}+1\right)}\cdot\dfrac{x+\sqrt{x}+1}{\sqrt{x}+2}\\ B=\dfrac{\sqrt{x}-1}{\left(\sqrt{x}-1\right)\left(\sqrt{x}+2\right)}=\dfrac{1}{\sqrt{x}+2}\\ b,x=4+2\sqrt{3}\Leftrightarrow\sqrt{x}=\sqrt{\left(\sqrt{3}+1\right)^2}=\sqrt{3}+1\\ \Leftrightarrow B=\dfrac{1}{\sqrt{3}+1+2}=\dfrac{1}{\sqrt{3}+3}=\dfrac{3-\sqrt{3}}{6}\\ c,B=\dfrac{1}{\sqrt{x}+2}\le\dfrac{1}{0+2}=\dfrac{1}{2}\\ B_{max}=\dfrac{1}{2}\Leftrightarrow x=0\)

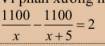
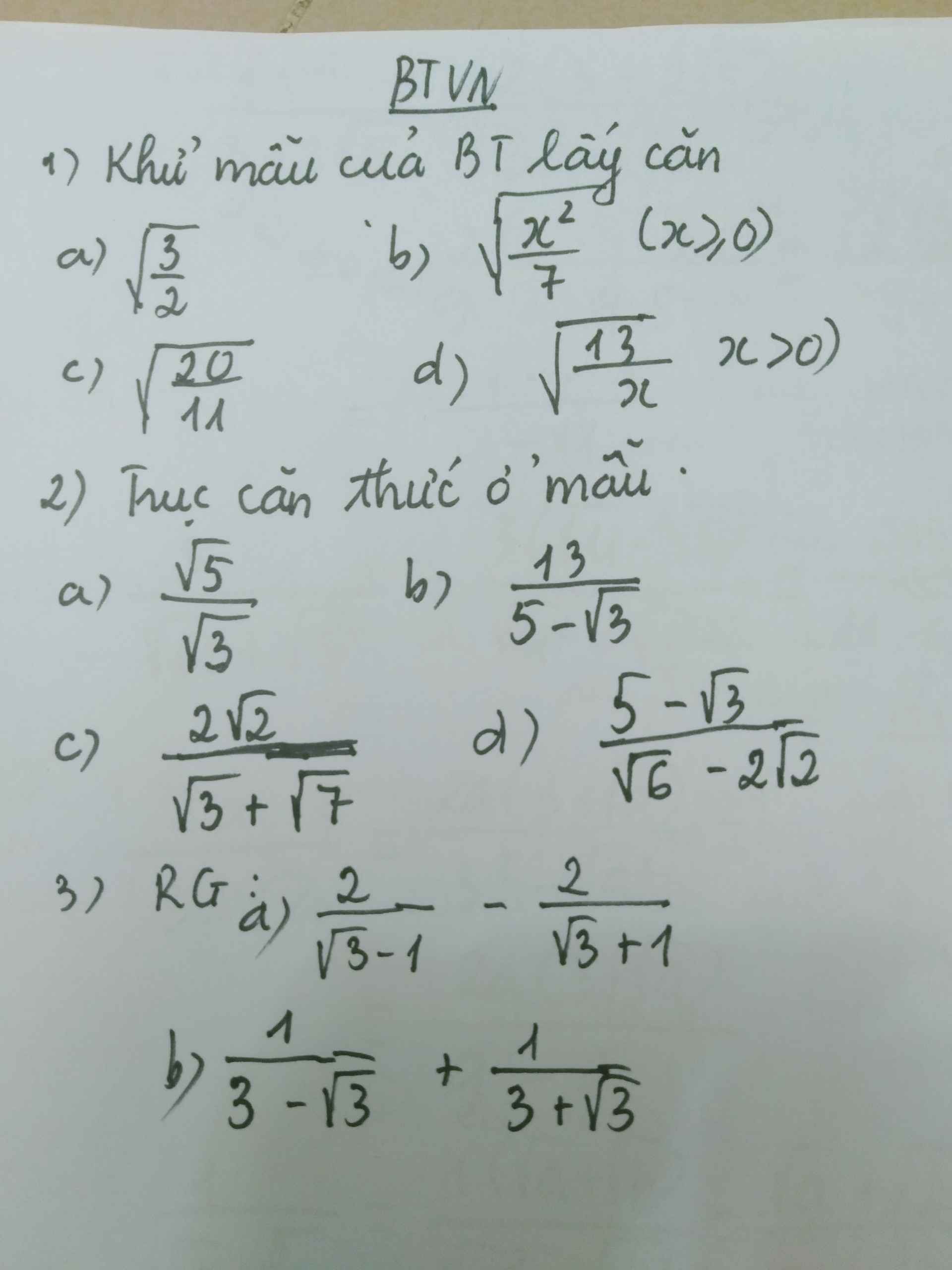


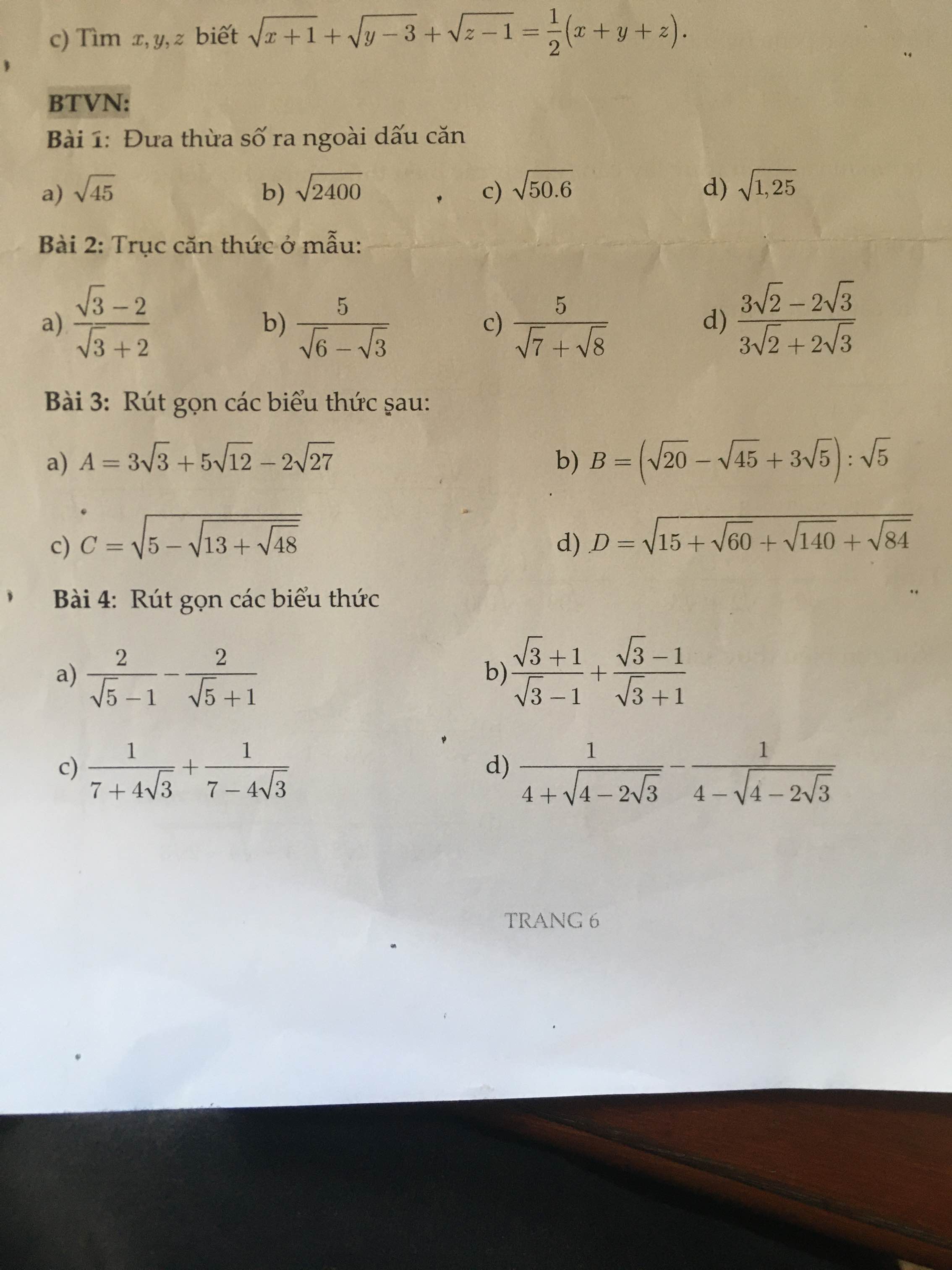


 HELP ME
HELP ME
705:
Gọi số tiền Bình và Minh có ban đầu lần lượt là a,b
Theo đề, ta có hệ:
a-b=100000 và a-120000=1/3(b+200000)
=>a-b=100000 và a-1/3b=200000/3+120000=560000/3
=>a=230000 và b=130000
=>Tổng số tiền là 360000 đồng