Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

a)
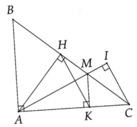
Ta có: ΔABC cân tại A(gt)
mà AM là đường phân giác ứng với cạnh đáy BC(gt)
nên AM là đường cao ứng với cạnh BC(Định lí tam giác cân)
\(\Leftrightarrow AM\perp BC\)
Xét ΔABC có
AM là đường cao ứng với cạnh BC(cmt)
BK là đường cao ứng với cạnh AC(Gt)
AM cắt BK tại I(Gt)
Do đó: I là trực tâm của ΔBAC(Tính chất ba đường cao của tam giác)
Suy ra: CI\(\perp\)AB(Đpcm)

a) Tam giác ABC cân tại A có AM là phân giác, do đó AM cũng là đường cao
AM vuông góc với BC
Lại có BK vuông góc với AC
Do đó I là trực tâm của tam giác ABC
Vậy CI vuông góc với AB
b) Tam giác BDH = tam giác DBP (ch.gn)
Do đó BH = DP
BDKQ là hình chữ nhật => DP = HK
=> BK = BH + HK = DP + DQ (đpcm)

a: Xét ΔABC có
AM,BK là đường cao
AM cắt BK tại I
=>I là trực tâm
=>CI vuông góc AB tại N
b:
Xet ΔAKB vuông tại K và ΔANC vuông tại N có
AB=AC
góc KAB chung
=>ΔAKB=ΔANC
=>BK=CN
DP//NC
=>DP/NC=BD/BC
=>DP/BK=BD/BC
DQ//BK
=>DQ/BK=CD/CB
=>DQ+DP=BK(BD/BC+CD/CB)=BK

BH=CK=căn 10^2-6^2=8cm
DF//KC
=>DF/KC= BD/BC
=>DF=BD/BC*8
DE//BH
=>DE/BH=CD/CB
=>DE=CD/CB*8
=>DF+DE=8

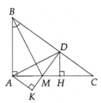
a) Chú ý tam giác ABD cân tại B nên BM là đường phân giác cũng là đường cao, từ đó B M ⊥ A D .
b) Chú ý AK, BM, DH là ba đường cao của tam giác AMD.

b) Xét ΔABH vuông tại H và ΔACH vuông tại H có
AB=AC(ΔABC cân tại A)
AH chung
Do đó: ΔABH=ΔACH(cạnh huyền-cạnh góc vuông)
Suy ra: BH=CH(hai cạnh tương ứng)
Xét ΔIBH vuông tại H và ΔICH vuông tại H có
BH=CH(cmt)
IH chung
Do đó: ΔIBH=ΔICH(hai cạnh góc vuông)
Suy ra: IB=IC(hai cạnh tương ứng)
Xét ΔIBC có IB=IC(cmt)
nên ΔIBC cân tại I(Định nghĩa tam giác cân)
Ta có: ΔIKC vuông tại K(gt)
nên IC là cạnh lớn nhất(Do IC là cạnh huyền)
hay IK<IC
mà IB=IC(cmt)
nên IK<IB
c) Ta có: ΔKBC vuông tại K(gt)
nên \(\widehat{KBC}+\widehat{KCB}=90^0\)(hai góc nhọn phụ nhau)
hay \(\widehat{KBC}+\widehat{ACB}=90^0\)(1)
Ta có: \(\widehat{DBC}+\widehat{ABC}=\widehat{ABD}\)(tia BC nằm giữa hai tia BA,BD)
nên \(\widehat{DBC}+\widehat{ABC}=90^0\)(2)
Từ (1) và (2) suy ra \(\widehat{KBC}=\widehat{DBC}\)
hay BC là tia phân giác của \(\widehat{KBD}\)(đpcm)