Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

a,
Ta có :
Δ ABC vuông tại A
Mà AI là đường trung tuyến của BC
=> AI = BI = IC
Xét Δ AIB, có :
AI = BI (cmt)
=> Δ AIB cân tại A
Xét Δ AIC, có :
AI = AC (cmt)
=> Δ AIC cân tại I

a). Ta có AM là đường trung trực của đoạn thẳng BC => AM\(\perp\) BC và BM=CM
Xét tam giác AMB vuông tại M và tam giác AMC vuông tại M có:
AM là cạnh chung.
BM=CM (cmt)
=> Tam giác AMB=tam giác AMC (hai cạnh góc vuông)
b). Tam giác AMB=tam giác AMC
=> AB=AC (hai cạnh tương ứng)
=> \(\widehat{BAM}\) = \(\widehat{CAM}\) (hai góc tương ứng)
=> \(\widehat{ABM}=\widehat{ACM}\) (hai góc tương ứng)
c). Xét tam giác ANB và tam giác ANC có:
AB=AC (cmt)
\(\widehat{BAN}=\widehat{CAN}\) (\(\widehat{BAM}=\widehat{CAM};N\in\) AM)
AN là cạnh chung.
=> Tam giác ANB=tam giác ANC (c.g.c)

Ta có hình vẽ ( bạn tự vẽ hình nha! )
a,
Vì đường trung trực của AB cắt BC tại N
=> N Cách đều 2 đầu mút A và B của đoạn AB
=> AN = AB
=> Tam giác ANB cân
Vì đường trung trực của AC cắt BC tại M
=> M Cách đều 2 đầu mút A và C của đoạn AC
=> AM = AC
=> Tam giác AMC cân
Vậy: ....
b,
VÌ tam giác AMC cân tại M Và tam giác ABN cân tại N
=> \(\widehat{MAC}=\widehat{NAB}=\widehat{ABC}\)
\(\Rightarrow\widehat{MAB}=\widehat{CAN}\)
Xét \(\Delta AMB\)và \(\Delta ANC\)có:
\(\widehat{MAB}=\widehat{CAN}\)( theo trên )
AB = AC ( vì tam giác ABC cân tại A )
\(\widehat{ABM}=\widehat{ACN}\)( vì kề bù với 2 góc bằng nhau )
=> \(\Delta AMB\)= \(\Delta ANC\)( g.c.g )
=> AM = AN ( 2 cạnh tương ứng ) ( 1 )
Vì \(\widehat{BAC}=\widehat{ACB}=\widehat{ABC}\) ( \(\Delta ABC\)cân tại A và \(\Delta MAC\)cân tại M )
=> \(\widehat{ABM}=\widehat{EAC}\)( vì kề bù với 2 góc bằng nhau )
Xét \(\Delta ABM\)và \(\Delta CAE\)có :
AB = AC ( theo trên )
\(\widehat{ABM}=\widehat{EAC}\)( theo trên )
BM = AE ( GT )
=> \(\Delta ABM\)= \(\Delta CAE\)( c.g.c )
=> AM = EC ( 2 cạnh tương ứng ) ( 2 )
Từ (1) và (2); ta có: AM = EC = AN
Vậy:AM = EC = AN

a) Ta có: \(AM=MB=\dfrac{AB}{2}\)(M là trung điểm của AB)
\(AN=NC=\dfrac{AC}{2}\)(N là trung điểm của AC)
mà AB=AC(ΔABC cân tại A)
nên AM=MB=AN=NC
Xét ΔAMO vuông tại M và ΔANO vuông tại N có
AO chung
AM=AN(cmt)
Do đó: ΔAMO=ΔANO(cạnh huyền-cạnh góc vuông)
b) Ta có: ΔAMO=ΔANO(cmt)
nên \(\widehat{MAO}=\widehat{NAO}\)(hai góc tương ứng)
hay \(\widehat{BAH}=\widehat{CAH}\)
mà tia AH nằm giữa hai tia AB,AC
nên AH là tia phân giác của \(\widehat{BAC}\)
c) Xét ΔAHB và ΔAHC có
AB=AC(ΔABC cân tại A)
\(\widehat{BAH}=\widehat{CAH}\)(cmt)
AH chung
Do đó: ΔAHB=ΔAHC(c-g-c)
Suy ra: HB=HC(hai cạnh tương ứng)
Ta có: ΔAHB=ΔAHC(cmt)
nên \(\widehat{AHB}=\widehat{AHC}\)(hai góc tương ứng)
mà \(\widehat{AHB}+\widehat{AHC}=180^0\)(hai góc kề bù)
nên \(\widehat{AHB}=\widehat{AHC}=\dfrac{180^0}{2}=90^0\)
hay \(AH\perp BC\)(đpcm)
Hình vẽ : tự vẽ
a) Ta có : tan giác ABC cân tại A ( gt )
\(\Rightarrow\) \(\left\{{}\begin{matrix}AB=AC\\\widehat{B}=\widehat{C}\end{matrix}\right.\)( t/c \(\Delta\) cân )
Ta có : AB = AC ( cmt )
Mà : M là trung điểm của AB ( gt ), N là trung điểm của AC ( gt )
\(\Rightarrow\dfrac{1}{2}AB=\dfrac{1}{2}AC\)
\(\Rightarrow AM=AN\)
Xét : \(\Delta\)AMO và \(\Delta\)ANO có
Cạnh AO chung
AM =AN (cmt )
\(\widehat{AMO}=\widehat{ANO}=90^0\left(CM\perp AB,BN\perp AC\right)\)
\(\Rightarrow\Delta AMO=\Delta ANO\left(ch-cgv\right)\)
b) Có \(\Delta AMO=\Delta ANO\left(cmt\right)\)
\(\Rightarrow\widehat{MAO}=\widehat{NAO}\) ( 2 cạnh tương ứng )
Ta có :
\(\widehat{MAO}=\widehat{NAO}\left(cmt\right)\)
Mà : Tia AH nằm giữa tia AB và tia AC
\(\Rightarrow\) AH là tia phân giác của \(\widehat{A}\) ( đpcm )
c) Ta có :
\(\Delta ABC\) cân tại A ( gt ), AH là tia phân giác của \(\widehat{A}\) ( cmt )
\(\Rightarrow\) AH cùng là đường cao và trung truyến
\(\Rightarrow\left\{{}\begin{matrix}AH\perp BC\\HB=HC\end{matrix}\right.\)( tính chất đường cao và trung tuyến )
d) Ta có :
\(AH\perp BC\left(cmt\right)\)
\(\Rightarrow\widehat{OHC}=90^0\)
\(\Rightarrow\)OC lớn hơn HC
Mà HC = HB ( cmt )
\(\Rightarrow\) OC lớn hơn HB ( đpcm )
-Hết-

a: O nằm trên trung trực của AB,AC
=>OA=OB và OA=OC
=>OB=OC
mà AB=AC
nên AO là trung trực của BC
b: D nằm trên trung trực của AB
=>DA=DB
=>góc DAB=góc DBA
E nằm trên trung trực của AC
=>EA=EC
=>góc EAC=góc ECA=góc DBA=góc DAB
Xét ΔDAB và ΔEAC có
góc DAB=góc EAC
AB=AC
góc B=góc C
=>ΔDAB=ΔEAC
=>BD=CE
c: Xét ΔOBD và ΔOCE có
OB=OC
góc OBD=góc OCE
BD=CE
=>ΔOBD=ΔOCE
=>OD=OE


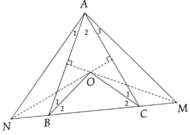
TK
lỗi ạ :> cả 2 hình bên dưới :>