Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

\(MK=\frac{MP}{2}\Rightarrow MK=PK\)
Hai tg MHK và tg PHK có chung đường cao từ H->MP và MK=PK nên \(S_{MHK}=S_{PHK}\)
Hai tg trên có chung cạnh HK nên đường cao từ M->HQ = đường cao từ P->HQ
Hai tg MHQ và tg PHQ có chung HQ và đường cao từ M->HQ = đường cao từ P->HQ \(\Rightarrow S_{MHQ}=S_{PHQ}\)
Ta có \(PQ=\frac{NP}{4}\Rightarrow\frac{PQ}{NQ}=\frac{1}{3}\)
Hai tg PHQ và tg NHQ có chung đường cao từ H->NP nên
\(\frac{S_{PHQ}}{S_{NHQ}}=\frac{PQ}{NQ}=\frac{1}{3}\) Mà \(S_{MHQ}=S_{PHQ}\Rightarrow\frac{S_{MHQ}}{S_{NHQ}}=\frac{1}{3}\)
Hai tg MHQ và tg NHQ có chung đường cao từ Q->HN nên
\(\frac{S_{MHQ}}{S_{MHQ}}=\frac{MH}{NH}=\frac{1}{3}\Rightarrow\frac{MH}{MN}=\frac{1}{2}\)
Hai tg MHK và tg MNK có chung đường cao từ K->HN nên
\(\frac{S_{MHK}}{S_{MNK}}=\frac{MH}{MN}=\frac{1}{2}\Rightarrow S_{MNK}=2xS_{MHK}\)
Hai tg MNK và MNP có chung đường cao từ N->MP nên
\(\frac{S_{MNK}}{S_{MNP}}=\frac{MK}{MP}=\frac{1}{2}\Rightarrow S_{MNP}=2xS_{MNK}=2.2.S_{MHK}=4x6=24cm^2\)

TK
Hai tg MHK và tg PHK có chung đường cao từ H->MP và MK=PK nên
Hai tg trên có chung cạnh HK nên đường cao từ M->HQ = đường cao từ P->HQ
Hai tg MHQ và tg PHQ có chung HQ và đường cao từ M->HQ = đường cao từ P->HQ
Ta có
Hai tg PHQ và tg NHQ có chung đường cao từ H->NP nên
Mà

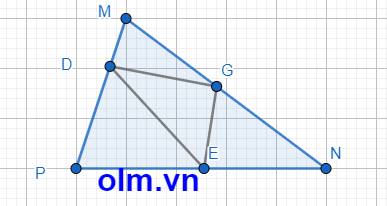
Tỉ số diện tích tam giác PDE và diện tích tứ giác DMNE là:
1 : 2 = \(\dfrac{1}{2}\)
Ta có sơ đồ: 
Theo sơ đồ ta có: Diện tích tam giác BDE = 360 : (1+2) = 120 (cm2)
Diện tích tứ giác DMNE là: 360 - 120 = 240 (cm2)
SMEP = \(\dfrac{1}{2}\)SMNP vì ( hai tam giác có chung đường cao hạ từ đỉnh M xuống đáy PN và PE = \(\dfrac{1}{2}\) PN)
SMEP = 360 \(\times\) \(\dfrac{1}{2}\) = 180(cm2)
Tỉ số diện tích SDEP và SMEP là: 120 : 180 = \(\dfrac{2}{3}\) ⇒ PD = \(\dfrac{2}{3}\) PM ( vì hai tam giác có chung đường cao hạ từ đỉnh E xuống đáy PM nên tỉ số diện tích hai tam giác là tỉ số của hai cạnh đáy)
Cạnh MD bằng: 1 - \(\dfrac{2}{3}\) = \(\dfrac{1}{3}\) (cạnh PM)
SMGD = \(\dfrac{1}{3}\) SMGP ( Vì hai tam giác có chung đường cao hạ từ đỉnh G xuống đáy PM và MD = \(\dfrac{1}{3}\) PM)
SMGP = \(\dfrac{1}{2}\) SMNP ( Vì hai tam giác có chung đường cao hạ từ đỉnh P xuống đáy MN và MG = \(\dfrac{1}{2}\) MN)
⇒ SMGP = \(\dfrac{1}{3}\) \(\times\) \(\dfrac{1}{2}\) SMNP = \(\dfrac{1}{3}\) \(\times\) \(\dfrac{1}{2}\) \(\times\) 360 = 60 (cm2)
SGEN = \(\dfrac{1}{2}\)SGPN ( vì hai tam giác có chung đường cao hạ từ đỉnh G xuông đáy PN và EN = \(\dfrac{1}{2}\)PN)
Tương tự ta có: SGPN = \(\dfrac{1}{2}\) SMNP
⇒ SGEN = \(\dfrac{1}{2}\) \(\times\) \(\dfrac{1}{2}\) \(\times\) 360 = 90 (cm2)
SGDE = SMNED - SMGD - SGEN = 240 - 60 -90 = 90 (cm2)
Đáp số: 90 cm2