Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

- Hình vẽ:
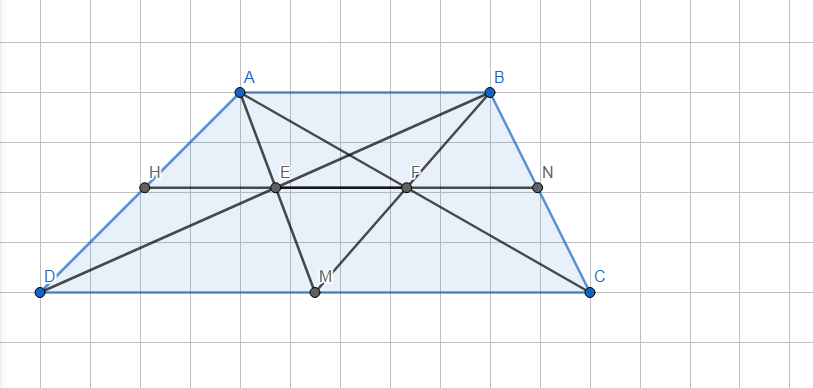
a) - Xét △EDM có:
AB//DM (ABCD là hình thang có 2 đáy là AB và CD).
=>\(\dfrac{AE}{EM}=\dfrac{AB}{DM}\) (định lí Ta-let) (1).
- Xét △FCM có:
AB//CM (ABCD là hình thang có 2 đáy là AB và CD).
=>\(\dfrac{BF}{MF}=\dfrac{AB}{CM}\) (định lí Ta-let) (2).
- Từ (1) và (2) và \(CM=DM\) (M là trung điểm BC) suy ra:
\(\dfrac{AE}{EM}=\dfrac{BF}{MF}\).
- Xét △ABM có:
\(\dfrac{AE}{EM}=\dfrac{BF}{MF}\) (cmt)
=>\(EF\)//\(AB\) (định lí Ta-let đảo)nên\(EF\)//\(AB\)//\(CD\)
b) -Xét △ADM có:
HE//DM (cmt).
=>\(\dfrac{HE}{DM}=\dfrac{AE}{AM}\) (định lí Ta-let). (3)
- Xét △ACM có:
EF//CM (cmt)
=>\(\dfrac{EF}{CM}=\dfrac{AE}{AM}\) (định lí Ta-let) (4)
- Từ (3) và (4) và \(DM=CM\) (M là trung điểm BC) suy ra: \(HE=EF\)
-Xét △BDM có:
EF//DM (cmt).
=>\(\dfrac{EF}{DM}=\dfrac{BF}{BM}\)(định lí Ta-let). (5)
- Xét △BCM có:
NF//CM (cmt)
=>\(\dfrac{NF}{CM}=\dfrac{BF}{BM}\) (định lí Ta-let) (6)
- Từ (5) và (6) và \(CM=DM\) (M là trung điểm BC) suy ra: \(NF=EF\)
Mà \(HE=EF\) nên \(HE=EF=NF=\dfrac{1}{3}HN\).
c) -Ta có: \(\dfrac{HE}{DM}=\dfrac{AE}{AM}\) (cmt)
=>\(\dfrac{DM}{HE}=\dfrac{AM}{AE}\).
=>\(\dfrac{DM}{HE}-1=\dfrac{EM}{AE}\) (7)
- Ta có: \(\dfrac{AE}{EM}=\dfrac{AB}{DM}\) nên \(\dfrac{EM}{AE}=\dfrac{DM}{AB}\). (8)
- Từ (7) và (8) suy ra:
\(\dfrac{DM}{HE}-1=\dfrac{DM}{AB}\)
=>\(\dfrac{DM}{HE}=\dfrac{DM}{AB}+1=\dfrac{DM+AB}{AB}\)
=>\(HE=\dfrac{AB.DM}{AB+DM}=\dfrac{7,5.\left(12.\dfrac{1}{2}\right)}{7,5+\left(12.\dfrac{1}{2}\right)}=\dfrac{10}{3}\)
=>\(HN=3HE=3.\dfrac{10}{3}=10\) (cm).

có m là trđ của cd rồi lại còn ef cắt bc tại m
a, xét tam giác DEM có AB // DM (gt) => ME/AE = DM/AB (ddl)
xét tam giác MFC có MC // AB (gt) => MF/FB = CM/AB (đl)
có DM = CM do M là trung điểm của CD (gt)
=> ME/AE = MF/FB xét tam giác ABM
=> EF // AB (đl)
b, gọi EF cắt AD;BC lần lượt tại P và Q
xét tam giác ABD có PE // AB => PE/AB = DE/DB (đl)
xét tam giác DEM có DM // AB => DE/DB = ME/MA (đl)
xét tam giác ABM có EF // AB => EF/AB = ME/MA (đl)
=> PE/AB = EF/AB
=> PE = EF
tương tự cm được FQ = EF
=> PE = EF = FQ
c, Xét tam giác DAB có PE // AB => PE/AB = DP/DA (đl)
xét tam giác ADM có PE // DM => PE/DM = AP/AD (đl)
=> PE/AB + PE/DM = DP/AD + AP/AD
=> PE(1/AB + 1/DM) = 1 (1)
xét tam giác AMB có EF // AB => EF/AB = MF/MB (đl)
xét tam giác BDM có EF // DM => EF/DM = BF/BM (đl)
=> EF/AB + EF/DM = MF/MB + BF/BM
=> EF(1/AB + 1/DM) = 1 (2)
xét tam giác ABC có FQ // AB => FQ/AB = CQ/BC (đl)
xét tam giác BMC có FQ // MC => FQ/MC = BQ/BC (đl)
=> FQ/AB + FQ/MC = CQ/BC + BQ/BC
có MC = DM (câu a)
=> FQ(1/AB + 1/DM) = 1 (3)
(1)(2)(3) => (1/AB + 1/DM)(PE + EF + FQ) = 3
=> PQ(1/AB + 1/DM) = 3
DM = 1/2 CD = 6
đến đây thay vào là ok

a/ Có AB // DM
=> t/g ABE đồng dạng t/g MDE (đ/l)
=> AE/ME = AB/MD = AB/MC (1)
Có AB // CM
=> t/g ABF đồng dạng t/g CMF (đ/l)
=> AF/MF = AB/CM (2)(1) ; (2)
=> AE/ME = AF/MF
Xét t/g AMB có AE/ME=AF/MF
=> EF // BC (Thales đảo)
b/ Xét t/g DEM có AB // DM
=> ME/AM = DM/AB (Hệ quả đ.l Thales)
Xét t/g AMB có EF // AB
=> ME/AM = EF/AB (Hệ quả Thales)
Do đó EF = DM = 1/2DC = 6 (cm)P/s: câu b không chắc lắm.
a) Ta có: AB//CD(AB và CD là hai đáy của hình thang ABCD)
nên AB//MC
Xét ΔAFB và ΔCFM có
\(\widehat{FAB}=\widehat{FCM}\)(hai góc so le trong, AB//MC)
\(\widehat{AFB}=\widehat{CFM}\)(hai góc đối đỉnh)
Do đó: ΔAFB\(\sim\)ΔCFM(g-g)
nên \(\dfrac{FA}{FC}=\dfrac{FB}{FM}=\dfrac{AB}{CM}\)
mà CM=DM(M là trung điểm của CD)
nên \(\dfrac{BF}{FM}=\dfrac{AB}{DM}\)(1)
Ta có: AB//CD(Hai cạnh đáy của hình thang ABCD)
nên AB//DM
Xét ΔABE và ΔMDE có
\(\widehat{ABE}=\widehat{MDE}\)(hai góc so le trong, AB//DM)
\(\widehat{AEB}=\widehat{MED}\)(hai góc đối đỉnh)
Do đó: ΔABE\(\sim\)ΔMDE(g-g)
nên \(\dfrac{AB}{DM}=\dfrac{AE}{EM}\)(2)
Từ (1) và (2) suy ra \(\dfrac{BF}{FM}=\dfrac{AE}{EM}\)
Xét ΔAMB có
E\(\in\)AM(Gt)
F\(\in\)BM(gt)
\(\dfrac{BF}{FM}=\dfrac{AE}{EM}\)(cmt)
Do đó: EF//AB(Định lí Ta lét đảo)

Gọi \(N\) là trung điểm của đoạn thắng \(AB\) \(;\) \(N'\) là giao điểm của \(GM\) và \(AB\)
Tứ giác \(ABCD\) là hình thang nên \(AB\text{//}CD\)
Khi đó,
\(\Delta GMD\) có \(AN'\text{//}MD\), nên \(\frac{AN'}{MD}=\frac{GN'}{GM}\) (hệ quả của định lý Ta-lét) \(\left(3\right)\)
\(\Delta GMC\) có \(N'B\text{//}MC\), nên \(\frac{N'B}{MC}=\frac{GN'}{GM}\) \(\left(4\right)\)
\(\left(3\right);\) \(\left(4\right)\) \(\Rightarrow\) \(\frac{AN'}{MD}=\frac{N'B}{MC}\) \(\left(=\frac{GN'}{GM}\right)\)
Mà \(MD=MC\) \(\left(gt\right)\), do đó, \(AN'=N'B\) hay \(N'\) phải trùng với \(N\)
Tức là ba điểm \(G,\) \(N,\) \(M\) thẳng hàng \(\left(\text{*}\right)\)
Tương tự, ta cũng chứng minh được ba điểm \(N,\) \(O,\) \(M\) thẳng hàng \(\left(\text{**}\right)\)
Từ \(\left(\text{*}\right)\) và \(\left(\text{**}\right)\) suy ra bốn điểm \(G,\) \(N,\) \(O,\) \(M\) thẳng hàng
Vậy, đoạn thẳng \(GO\) sẽ lần lượt đi qua \(N\) và \(M\) hay đi qua trung điểm của \(AB\) và \(CD\)
Đặt AB = m, MC = MD = n.
a) Do AB // CD, ta có :
\(\frac{MI}{TA}=\frac{MD}{AB}=\frac{n}{m}\)
\(\frac{MK}{KB}=\frac{MC}{AB}=\frac{n}{m}\)
Từ (1) và (2) suy ra \(\frac{MI}{IA}=\frac{MK}{KB}\) Từ đó theo định lí đảo của định lí Ta - lét đối với tam giác MAB, ta có IK // AB. ( nhưng lớp 8 chưa học ta -lét thì fai )