Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

Bài 3:
a: Xét ΔAIB và ΔCID có
IA=IC
góc AIB=góc CID
IB=ID
Do đó: ΔAIB=ΔCID
b: Xét tứ giác ABCD có
I là trung điểm chung của AC và BD
nên ABCD là hình bình hành
Suy ra: AD//BC va AD=BC
Bài 6:
a: Xét ΔADB và ΔAEC có
AD=AE
góc A chung
AB=AC
Do đó: ΔADB=ΔAEC
SUy ra: BD=CE
b: Xét ΔEBC và ΔDCB có
EB=DC
BC chung
EC=BD
Do đó: ΔEBC=ΔDCB
Suy ra: góc OBC=góc OCB
=>ΔOBC cân tại O
=>OB=OC
=>OE=OD
=>ΔOED cân tại O
c: Xét ΔABC có AE/AB=AD/AC
nên ED//BC

a: Xét ΔHBA vuông tại H và ΔABC vuông tại A có
góc B chung
Do đó: ΔHBA\(\sim\)ΔABC
b: \(BC=\sqrt{6^2+8^2}=10\left(cm\right)\)
\(AH=\dfrac{AB\cdot AC}{BC}=4.8\left(cm\right)\)

Bài 1 : Bài giải
a, Trong \(\Delta ABC\) vuông tại A có :
\(AB^2+AC^2=BC^2\text{ }\Rightarrow\text{ }9^2+12^2=81+144=225=BC^2\text{ }\Rightarrow\text{ }BC=5\text{ }cm\)
b, Vì BD là đường phân giác \(\widehat{ABC}\) nên : \(\widehat{B_1}=\widehat{B_2}\)
Xét 2 tam giác \(\Delta ABD\) vuông tại A và \(\Delta AED\) vuông tại E có :
\(BD\) : cạnh huyền - cạnh chung
\(\widehat{B_1}=\widehat{B_2}\) ( cmt )
\(\Rightarrow\text{ }\Delta ABD=\Delta AED\text{ }\left(ch-gn\right)\)
\(\Rightarrow\text{ }AD=DE\text{ }\left(2\text{ cạnh tương ứng }\right)\)
\(\Rightarrow\text{ }\Delta DAE\text{ cân }\)
c, Trong \(\Delta DEC\text{ }\) vuông tại E có : DC là cạnh đối diện với \(\widehat{E}\) nên \(DC\) là cạnh có độ dài lớn nhất \(\Rightarrow\text{ }DE< DC\)
Mà \(DA=DE\text{ nên }DA< DC\)
d, Vì \(\hept{\begin{cases}DE\text{ }\perp\text{ }BC\\BF\text{ }\perp\text{ }CF\\AB\text{ }\perp\text{ }AC\end{cases}}\text{ }\Rightarrow\text{ }DE\text{ , }AB\text{ và }BF\text{ là đường cao của }\Delta OBC\)
\(\Rightarrow\text{ }AB\text{, }DE\text{ và }CF\text{ đồng quy tại 1 điểm}\)

a: Xét ΔHBA vuông tại H và ΔABC vuông tại A có
\(\widehat{B}\) chung
Do đó: ΔHBA\(\sim\)ΔABC
Xét ΔHBA vuông tại H và ΔHAC vuông tại H có
\(\widehat{HBA}=\widehat{HAC}\)
Do đó: ΔHBA\(\sim\)ΔHAC
b: Xét ΔABC vuông tại A có AH là đường cao
nên \(\left\{{}\begin{matrix}AB^2=BH\cdot BC\\AH^2=HB\cdot HC\end{matrix}\right.\)(hệ thức lượng)
c: \(AB=\sqrt{BC^2-AC^2}=12\left(cm\right)\)
\(AH=\dfrac{AB\cdot AC}{BC}=\dfrac{12\cdot16}{20}=9.6\left(cm\right)\)
\(BH=\sqrt{AB^2-AH^2}=7.2\left(cm\right)\)
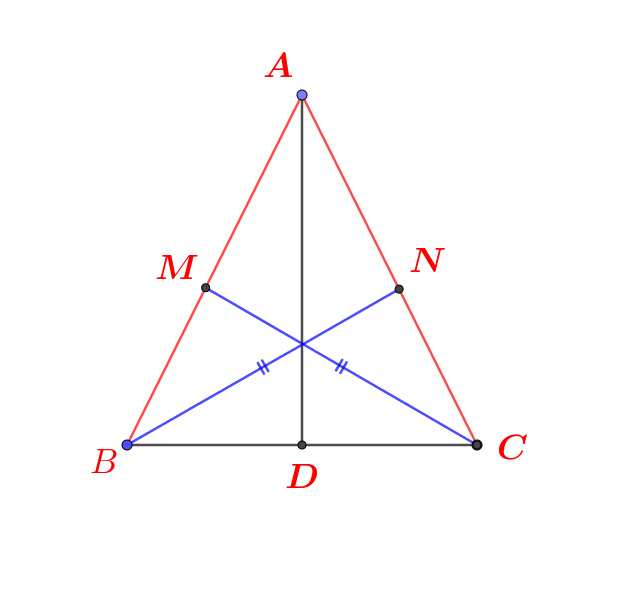
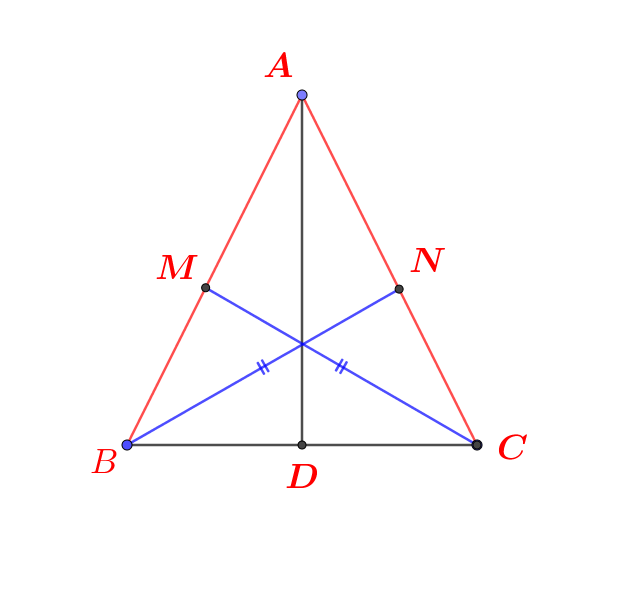
*Qua C, kẻ đường thẳng song song với AB cắt AD tại E.
- Xét △ABD có: \(AB\)//\(CE\) (gt)
=>\(\dfrac{AB}{CE}=\dfrac{BD}{CD}\) (định lí Ta-let).
Mà \(\dfrac{AB}{AC}=\dfrac{BD}{CD}\) (gt)
=>\(\dfrac{AB}{CE}=\dfrac{AB}{AC}\) hay \(CE=AC\).
=>△ACE cân tại C.
=>\(\widehat{EAC}=\widehat{AEC}\).
Mà\(\widehat{AEC}=\widehat{BAD}\) ( \(AB\)//\(CE\) và so le trong).
=>\(\widehat{EAC}=\widehat{BAD}\) hay AD là phân giác của \(\widehat{BAC}\).
Xét tg ABC có
\(\dfrac{BD}{CD}=\dfrac{AB}{AC}\left(gt\right)\)
=>AD là đường phân giác