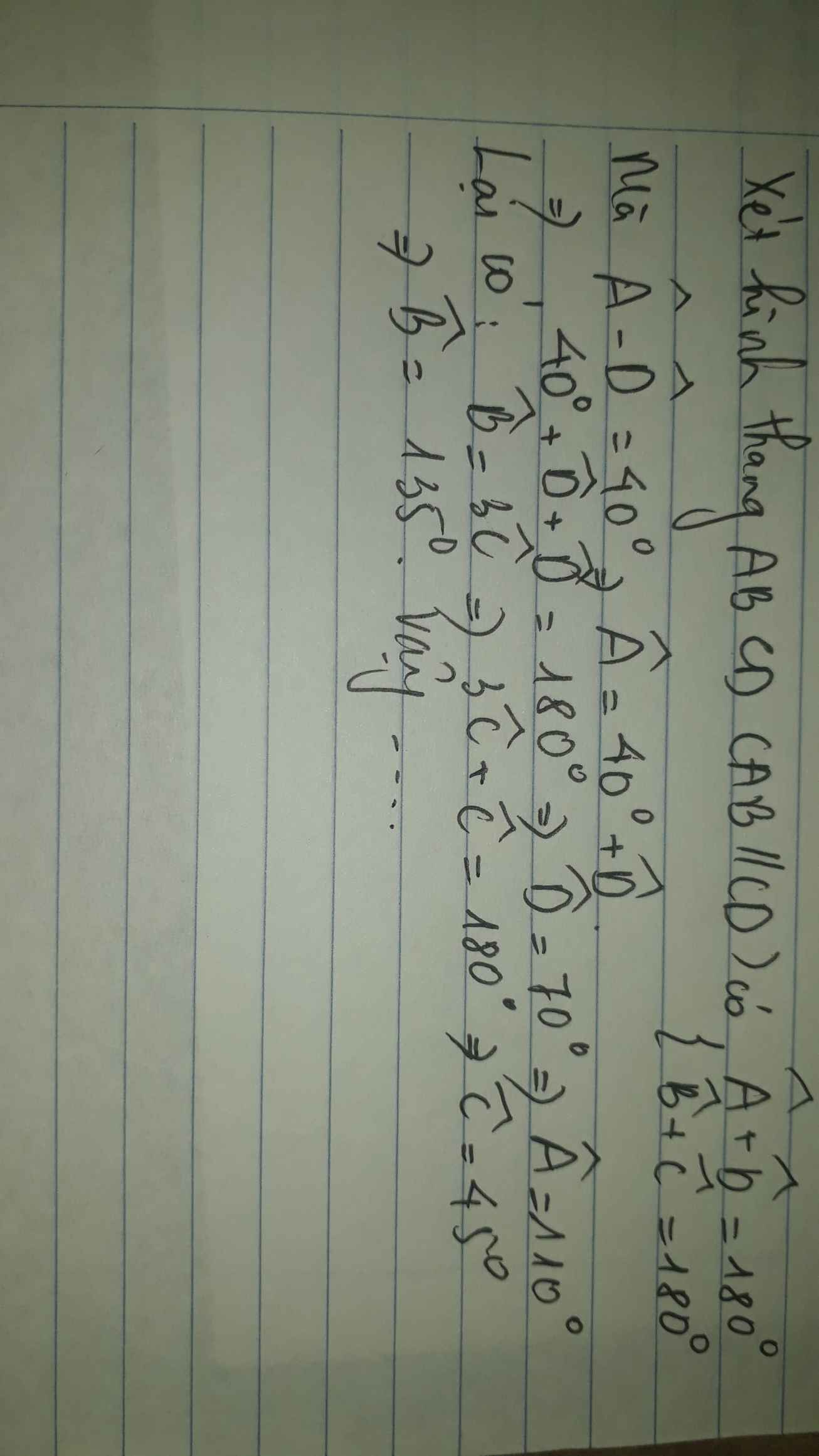Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

Bài 3:
a: Ta có: \(\widehat{OAB}=\widehat{ODC}\)
\(\widehat{OBA}=\widehat{OCD}\)
mà \(\widehat{ODC}=\widehat{OCD}\)
nên \(\widehat{OAB}=\widehat{OBA}\)
Xét ΔOAB có \(\widehat{OAB}=\widehat{OBA}\)
nên ΔOAB cân tại O

Bài 3:
a: Ta có: \(\widehat{OAB}=\widehat{ODC}\)
\(\widehat{OBA}=\widehat{OCD}\)
mà \(\widehat{ODC}=\widehat{OCD}\)
nên \(\widehat{OAB}=\widehat{OBA}\)
Xét ΔOAB có \(\widehat{OAB}=\widehat{OBA}\)
nên ΔOAB cân tại O

Kéo dài DA,cắt BC tại E
Ta có:Xét tam giác DBE và tam giác DBC có:
\(\hept{\begin{cases}\widehat{DBE}=\widehat{DBC}=\left(=90^0\right)\\DBchung\\\widehat{BDE}=\widehat{BDC}\left(gt\right)\end{cases}}\)
\(\Rightarrow\Delta DBE=\Delta DBC\left(g.c.g\right)\)
\(\Rightarrow\widehat{DEB}=\widehat{DCB}\left(1\right)\)
Ta lại có:Vì tứ giác ABCD là hình thang cân có AB song song với CD nên
\(\Rightarrow\widehat{ADC}=\widehat{BCD}\left(2\right)\)
Từ (1) và (2)
Suy ra tam giác DEC là tam giác đều
\(\Rightarrow\widehat{ADC}=\widehat{BCD}=60^0\)
\(\Rightarrow\widehat{DAB}=\widehat{CBA}=\frac{360^0-60^0.2}{2}=120^0\)
Vậy............

Bài 4:
Xét ΔAED vuông tại E và ΔBFC vuông tại F có
AD=BC
góc D=góc C
Do đó: ΔAED=ΔBFC
=>DE=CF
Bài 3:
a: Xét ΔADC và ΔBCD có
AD=BC
AC=BD
DC chung
Do đó: ΔADC=ΔBCD
=>góc ACD=góc BDC
b: Ta co: góc ACD=góc BDC
=>góc EAB=góc EBA
=>ΔEAB cân tại E

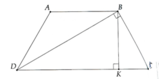
a) DDBC vuông có B C D ^ = 2 B D C ^ nên A D C ^ = B C D ^ = 60 0 và D A B ^ = C B A ^ = 120 0
b) Tính được DC = 2.BC = 12cm, suy ra PABCD = 30cm.
Hạ đường cao BK, ta có BK = 3 3 c m .
Vậy SABCD = 27 3 c m 2