Bài 3. Xem hình 2.a) Kể tên các cặp đoạn thẳng song song. Giải thích tại sao?.b) Tính các góc còn lại trong hình vẽ biết...

K

Khách

Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

Chọn lớp

Chọn môn

Mua vip

TA

❖Tiến Anh亗『ʈєɑɱ❖๖ۣۜƝƘ☆』

9 tháng 9 2021 - olm

Bài 3. Xem hình 2.
a) Kể tên các cặp đoạn thẳng song song. Giải thích tại sao?.
b) Tính các góc còn lại trong hình vẽ biết \(\widehat{QPN}=95^O\)

1

PM

Phạm Minh Quân

9 tháng 9 2021

Hình đâu???

Các câu hỏi dưới đây có thể giống với câu hỏi trên

1H

15 Hoàng Khánh Linh

4 tháng 10 2021

Bài 1.Cho hình 1, biết abvà 45cAa=. Tính các góc còn lại trong hình vẽ.Hình 1Hình 2Bài 2.Xem hình 2.a) Kể tên các cặp đoạn thẳng song song. Giải thích tại sao?.b) Tính các góc còn lại trong hình vẽ biết 95QPN=.Bài 3.Cho hình vẽ bên, trong đó ab. Tính số đo x, y.ĐS: 110x=,...

0

Y

ỵyjfdfj

28 tháng 9 2021

Bai 2:Cho các hình vẽ dưới đây aFbEc43211234600120oa) Kể tên các cặp góc so le trong, đồng vị, trong cung phía.b) Tính \(F_1;F_2;F_3;F_4\) c) Hai đường thẳng a, b có song song với nhau không? Vì sao? ( nếu có giải thích bằng 2...

3

NH

Nguyễn Hoàng Minh

28 tháng 9 2021

\(a,\)So le trong: \(E_1 và F_2;E_2 và F_1\)

Đồng vị: \(E_1 và F_4;E_2 và F_3;E_3 và F_2;E_4 và F_1\)

Trong cùng phía: \(E_1 và F_1;E_2 và F_2\)

\(b,\widehat{F_1}=\widehat{F_3}=120^0\left(đối.đỉnh\right)\\ \widehat{F_2}+\widehat{F_3}=180^0\left(kề.bù\right)\Rightarrow\widehat{F_2}=180^0-120^0=60^0\\ \widehat{F_2}=\widehat{F_4}-60^0\left(đối.đỉnh\right)\)

\(c,C_1:\widehat{F_2}=\widehat{E_3}\left(=60^0\right)\)

Mà 2 góc này ở vị trí đồng vị nên \(a//b\)

\(C_2:\)\(\widehat{E_1}=\widehat{E_3}=60^0\left(đối.đỉnh\right)\Rightarrow\widehat{E_1}=\widehat{F_2}\left(=60^0\right)\)

Mà 2 góc này ở vị trí so le trong nên \(a//b\)

HP

hưng phúc

28 tháng 9 2021

a. Các cặp góc:

- So le trong là: \(\widehat{E_1}\) và \(\widehat{F_2};\widehat{E_2}\) và \(\widehat{F_1}\)

- Đồng vị là: \(\widehat{E_4},\widehat{F_1};\widehat{E_3},\widehat{F_2};\widehat{E_2},\widehat{F_3};\widehat{E_1},\widehat{F_4}\)

- Trong cùng phía là: \(\widehat{E_1},\widehat{F_1};\widehat{E_2},\widehat{F_2}\)

b. Ta có: \(\widehat{F_1}=\widehat{F_3}=120^o\) (đối đỉnh)

\(\widehat{F_2}=180^o-\widehat{F_1}=180^o-120^o=60^o\)

\(\widehat{F_3}=120^o\)

\(\widehat{F_4}=\widehat{F_2}=60^o\) (đối đỉnh)

c.

C₁: Ta có: \(\widehat{E_1}=\widehat{E_3}=60^o\) (đối đỉnh)

Ta thấy: \(\widehat{E_1}=\widehat{F_2}=60^o\)

=> a//b (so le trong)

C₂: Ta có: \(\widehat{E_2}=180^o-\widehat{E_3}=180^o-60^o=120^o\)

Ta thấy: \(\widehat{E_2}=\widehat{F_1}=120^o\)

=> a//b (so le trong)

PT

Pham Trong Bach

24 tháng 3 2017

Cho hình vẽ, biết:a) A 2 ^ = 70 0 ; B ^ = 110 0 . Chứng tỏ rằng Ax//Byb) F ^ = H ^ 1 ; K ^ = H ^ 2 . Chứng tỏ rằng EF//IKc) Cho hình vẽ, biết : M ^ 1 = 75 0 ; N ^ 1 = 105 0 ; P ^ 1 = 75 ...

1

CM

Cao Minh Tâm

24 tháng 3 2017

Cho hình vẽ, biết :

a) T a có: A ^ 1 = A ^ 2 = 70 0 (đối đỉnh).

Do đó A ^ 1 + B ^ = 70 0 + 110 0 = 180 0

Suy ra Ax//By (vì có cặp góc trong cùng phía bù nhau).

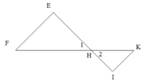
b) Ta có: F ^ = H ^ 1 ; K ^ = H ^ 2 mµ H ^ 1 = H ^ 2 ( đối đỉnh)

nên F ^ = K ^ . Suy ra EF//IK( vì có cặp góc so le trong bằng nhau).

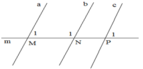
Ta có : M ^ 1 = P ^ 1 = 75 0 .

Suy ra a//c( vì có cặp góc đồng vị bằng nhau)

Ta có:

b N P ^ kÒ bï víi gãc N 1 , d o ®ã: b N P ^ = 180 0 − 105 0 = 75 0 VËy b N P ^ = P 1 ^ = 70 0

Suy ra b//c (vì có cặp góc đồng vị bằng nhau)

H

Huyenanh

19 tháng 9 2021

Bài 1: Vẽ 2 đường thẳng cắt nhau sao cho các góc tạo thành có 1 góc bằng 60°.Tính số đo các góc còn lại.Bài 2: Cho BOD, vẽ AOD kề bù BOD, vẽ tiếp AOC kề bù với AOD. Kể tên các cặp góc đối đỉnh trong hình vẽ và giải thích vì sao?Giúp mình 2 bài này với mình đang cần gấp mình cảm ơn...

0

HB

Hoàng Bắc Nguyệt

26 tháng 8 2018 - olm

Cho góc nhọn \(\widehat{xOy}\). Từ điểm A trên Ox vẽ AB vuông góc Oy tại B , BC vuông góc Ox tại C; CD vuông góc Oy tại D và DE vuông góc Ox tại E .

a, Kể tên những cặp đường thẳng song song .Vì sao?

b, Trong hình vẽ có những cặp góc nhọn nào bằng nhau . Vì sao?

Nhờ mọi người vẽ hình và giúp mk nha.

0

NV

Nguyen Van Tung

27 tháng 9 2018 - olm

Hai đường thẳng MN và PQ cắt nhau tại O, tao thẳng góc MOP có so đo 70^o

a)tính số đo các góc còn lại ?

b)vẽ Ot là phân giác của góc MÓP rồi vẽ Ot' là tia đối của tia Ot. Vì sao Ot' là phân giác của góc NOQ ?

c)kể tên các cặp góc đối đỉnh là góc nhọn ?

d)trong hình vẽ tạo thành có bao nhiêu cặp góc đối đỉnh nhỏ hơn góc bẹt?kể tên các cặp góc đo?

1

KT

Kotarou Tora

27 tháng 9 2018

a) Vì \(MOP-MOQ\) là hai góc kề bù, ta có :

\(MOQ=180^0_{ }-MOP=180^0_{ }-70^0_{ }\)

\(\Rightarrow MOQ=110^0_{ }\)

Áp dụng tính chất hai góc đối đỉnh, ta có :

\(MOP=NOQ\)

\(MOQ=PON\)

b) Vì \(Ot\) là tia phân giác của \(MOP\Rightarrow TOP=TOM=\frac{1}{2}MOP=\frac{110}{2}=55^0_{ }\)

Vì \(POT-QOT'\) là hai góc đối đỉnh \(\Rightarrow POT=QOT'=55^0_{ }\left(1\right)\)

Vì \(MOT-NOT'\)là hai góc đối đỉnh \(\Rightarrow MOT=NOT'=55^0_{ }\left(2\right)\)

Từ \(\left(1\right)-\left(2\right)\Rightarrow OT'\)là tia phân giác của \(NOQ\)

c) \(POT-QOT'\)

\(MOT-NOT'\)

\(POM-NOQ\)

N

nm0880232

3 tháng 9 2021 - olm

Bài toán 5: Vẽ đường tròn tâm O và các đường kính AB và CD. Kể tên các cặp góc đối đỉnh trong hình vẽ.Bài toán 6: Hai đường thẳng AB và CD cắt nhau tại O. Biết góc AOC+ góc BOD=103 độ.Tính số đo của bốn góc tạo thành.Bài toán 7: Hai đường thẳng MN và PQ cắt nhau tại O, tạo thành góc MOP =60 độa) Tính số đo của các góc còn lại;b) Vẽ tia Ot là tia phân giác của góc MOP rồi vẽ tia Ot’ là...

0