Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

$\begin{cases}\dfrac{1}{x}+\dfrac{1}{y}=\dfrac16\\\dfrac{10}{3x}+\dfrac{10}{y}=1\\\end{cases}$
`<=>` $\begin{cases}\dfrac{10}{x}+\dfrac{10}{y}=\dfrac53\\\dfrac{10}{3x}+\dfrac{10}{y}=1\\\end{cases}$
`<=>` $\begin{cases}\dfrac{1}{x}+\dfrac{1}{y}=\dfrac16\\\dfrac{20}{3}x=\dfrac23\\\end{cases}$
`<=>` $\begin{cases}x=\dfrac{1}{10}\\y=\dfrac{1}{15}\\\end{cases}$
Vậy `(x,y)=(1/10,1/15)`
\(\left\{{}\begin{matrix}\dfrac{1}{x}+\dfrac{1}{y}=\dfrac{1}{6}\\\dfrac{10}{3x}+\dfrac{10}{y}=1\end{matrix}\right.\left(x,y\ne0\right)\Rightarrow\left\{{}\begin{matrix}\dfrac{1}{x}+\dfrac{1}{y}=\dfrac{1}{6}\\\dfrac{10}{3}.\dfrac{1}{x}+10.\dfrac{1}{y}=1\end{matrix}\right.\)
\(\Rightarrow\left\{{}\begin{matrix}\dfrac{10}{x}+\dfrac{10}{y}=\dfrac{5}{3}\left(1\right)\\\dfrac{10}{3}.\dfrac{1}{x}+\dfrac{10}{y}=1\left(2\right)\end{matrix}\right.\)
Lấy \(\left(1\right)-\left(2\right)\Rightarrow\dfrac{20}{3}.\dfrac{1}{x}=\dfrac{2}{3}\Rightarrow\dfrac{1}{x}=\dfrac{1}{10}\Rightarrow x=10\)
\(\Rightarrow\dfrac{1}{y}=\dfrac{1}{6}-\dfrac{1}{10}=\dfrac{1}{15}\Rightarrow y=15\)

a) \(\left\{{}\begin{matrix}\dfrac{2x}{x+1}+\dfrac{y}{y+1}=2\\\dfrac{x}{x+1}+\dfrac{3y}{y+1}=-1\end{matrix}\right.\)(Đk: \(x\ne-1;y\ne-1\))
Đặt \(\dfrac{x}{x+1}\) là A
\(\dfrac{y}{y+1}\) là B
Ta có HPT mới : \(\left\{{}\begin{matrix}2A+B=2\\A+3B=-1\end{matrix}\right.\)(1)
Giải HPT (1) ta được A= \(\dfrac{7}{5}\) ; B=\(-\dfrac{4}{5}\)
+Với A=\(\dfrac{7}{5}\) ta có:
\(\dfrac{x}{x+1}=\dfrac{7}{5}\)
<=>\(5x=7x+7\)
<=>-2x=7
<=> x=\(-\dfrac{7}{2}\)
+Với B = \(-\dfrac{4}{5}\) ta có:
\(\dfrac{y}{y+1}=-\dfrac{4}{5}\)
<=>5y=-4y-4
<=>9y=-4
<=>y=\(-\dfrac{4}{9}\)
Vậy HPT có nghiệm (x;y) = \(\left\{-\dfrac{7}{2};-\dfrac{4}{9}\right\}\)

đặt \(\dfrac{1}{x+2}=a,\dfrac{1}{y+2}=b\)(\(x,y\ne-2\))
\(=>\left\{{}\begin{matrix}2a+b=1\\8a-5b=1\end{matrix}\right.=>\left\{{}\begin{matrix}a=\dfrac{1}{3}\\b=\dfrac{1}{3}\end{matrix}\right.\)
\(=>\left\{{}\begin{matrix}\dfrac{1}{x+2}=\dfrac{1}{3}\\\dfrac{1}{y+2}=\dfrac{1}{3}\end{matrix}\right.=>\left\{{}\begin{matrix}x=1\left(tm\right)\\y=1\left(tm\right)\end{matrix}\right.\)

Điều kiện : x ≠ -2 ;y ≠ -2
Đặt : \(\dfrac{1}{x+2}=a;\dfrac{1}{y+2}=b\)
Ta có :
\(hpt\text{⇔}\left\{{}\begin{matrix}2a+b=1\\8x-5b=1\end{matrix}\right.\text{⇔}\left\{{}\begin{matrix}a=\dfrac{1}{3}\\b=\dfrac{1}{3}\end{matrix}\right.\)
Suy ra:
\(\left\{{}\begin{matrix}x+2=3\\y+2=3\end{matrix}\right.\text{⇔}\left\{{}\begin{matrix}x=1\\y=1\end{matrix}\right.\)
Vậy nghiệm của hệ phương trình : (x ; y) = (1;1)
Ta có: \(\left\{{}\begin{matrix}\dfrac{2}{x+2}+\dfrac{1}{y+2}=1\\\dfrac{8}{x+2}-\dfrac{5}{y+2}=1\end{matrix}\right.\)
\(\Leftrightarrow\left\{{}\begin{matrix}\dfrac{8}{x+2}+\dfrac{4}{y+2}=4\\\dfrac{8}{x+2}-\dfrac{5}{y+2}=1\end{matrix}\right.\Leftrightarrow\left\{{}\begin{matrix}\dfrac{9}{y+2}=3\\\dfrac{2}{x+2}+\dfrac{1}{y+2}=1\end{matrix}\right.\)
\(\Leftrightarrow\left\{{}\begin{matrix}y+2=3\\\dfrac{2}{x+2}=1-\dfrac{1}{3}=\dfrac{2}{3}\end{matrix}\right.\Leftrightarrow\left\{{}\begin{matrix}y=1\\x=1\end{matrix}\right.\)
Vậy:(x,y)=(1;1)

a) ĐK xác định : x≠0;y≠0
ta có : \(\left\{{}\begin{matrix}\dfrac{5}{x}+\dfrac{6}{y}=9\\\dfrac{2}{x}-\dfrac{6}{y}=7\end{matrix}\right.\) <=> \(\left\{{}\begin{matrix}\dfrac{7}{x}=16\\\dfrac{2}{x}-\dfrac{6}{y}=7\end{matrix}\right.< =>\left\{{}\begin{matrix}x=\dfrac{7}{16}\\y=-\dfrac{42}{17}\end{matrix}\right.\)
Vậy S = {(\(\dfrac{7}{16};-\dfrac{42}{17}\))}
b) Đk xác định : x≠0;y≠0
ta có : \(\left\{{}\begin{matrix}\dfrac{5}{x}+\dfrac{1}{y}=14\\\dfrac{8}{x}-\dfrac{1}{y}=-8\end{matrix}\right.< =>\left\{{}\begin{matrix}\dfrac{13}{x}=6\\\dfrac{5}{x}+\dfrac{1}{y}=14\end{matrix}\right.\) <=> \(\left\{{}\begin{matrix}x=\dfrac{13}{6}\\y=\dfrac{13}{152}\end{matrix}\right.\)
Vậy S={(\(\dfrac{13}{6};\dfrac{13}{152}\))}
c) ĐK xác định : x≠0;y≠0
ta có : \(\left\{{}\begin{matrix}\dfrac{2}{x}+\dfrac{7}{y}=21\\-\dfrac{2}{x}-\dfrac{5}{y}=-11\end{matrix}\right.\) <=> \(\left\{{}\begin{matrix}\dfrac{2}{y}=10\\\dfrac{2}{x}+\dfrac{7}{y}=21\end{matrix}\right.< =>\left\{{}\begin{matrix}y=\dfrac{1}{5}\\x=-\dfrac{1}{7}\end{matrix}\right.\)
Vậy S={(\(-\dfrac{1}{7};\dfrac{1}{5}\))}
d) ĐK xác định : x≠0;y≠0
ta có : \(\left\{{}\begin{matrix}\dfrac{9}{x}+\dfrac{2}{y}=22\\\dfrac{5}{x}-\dfrac{2}{y}=13\end{matrix}\right.\) <=> \(\left\{{}\begin{matrix}\dfrac{14}{x}=35\\\dfrac{5}{x}-\dfrac{2}{y}=13\end{matrix}\right.< =>\left\{{}\begin{matrix}x=\dfrac{2}{5}\\y=-4\end{matrix}\right.\)
Vậy S={(0,4;-4)}
e) ĐKXĐ : x≠0;y≠0
ta có : \(\left\{{}\begin{matrix}\dfrac{3}{x}+\dfrac{5}{y}=10\\-\dfrac{3}{x}-\dfrac{7}{y}=8\end{matrix}\right.\) <=> \(\left\{{}\begin{matrix}-\dfrac{2}{y}=18\\\dfrac{3}{x}+\dfrac{5}{y}=10\end{matrix}\right.< =>\left\{{}\begin{matrix}y=-\dfrac{1}{9}\\x=\dfrac{3}{55}\end{matrix}\right.\) 'Vậy....

ĐK: \(x,y\neq 0\)
\(PT\left(2\right)\Leftrightarrow x=9-y\)
Thay vào \(PT\left(1\right)\Leftrightarrow\dfrac{1}{9-y}+\dfrac{1}{y}=\dfrac{1}{2}\Leftrightarrow2y+18-2y=9y-y^2\)
\(\Leftrightarrow y^2-9y+18=0\\ \Leftrightarrow\left[{}\begin{matrix}y=3\Rightarrow x=6\\y=6\Rightarrow x=3\end{matrix}\right.\)
Vậy \(\left(x;y\right)=\left(6;3\right);\left(3;6\right)\)
ĐK x;y \(\ne\)0
HPT <=> \(\left\{{}\begin{matrix}\dfrac{1}{x}+\dfrac{1}{y}=\dfrac{1}{2}\\x+y=9\end{matrix}\right.\Leftrightarrow\left\{{}\begin{matrix}\dfrac{x+y}{xy}=\dfrac{1}{2}\\x+y=9\end{matrix}\right.\Leftrightarrow\left\{{}\begin{matrix}xy=18\\x+y=9\end{matrix}\right.\)
<=> \(\left\{{}\begin{matrix}x\left(9-x\right)=18\\y=9-x\end{matrix}\right.\Leftrightarrow\left\{{}\begin{matrix}x^2-9x+18=0\\y=9-x\end{matrix}\right.\Leftrightarrow\left\{{}\begin{matrix}\left(x-3\right)\left(x-6\right)=0\\y=9-x\end{matrix}\right.\)
<=> \(\left\{{}\begin{matrix}\left[{}\begin{matrix}x=3\\x=6\end{matrix}\right.\\y=9-x\end{matrix}\right.\)
Khi x= 3 => y = 6
Khi x = 6 => y = 3
Vậy nghiệm phương trình là (3;6) ; (6;3)
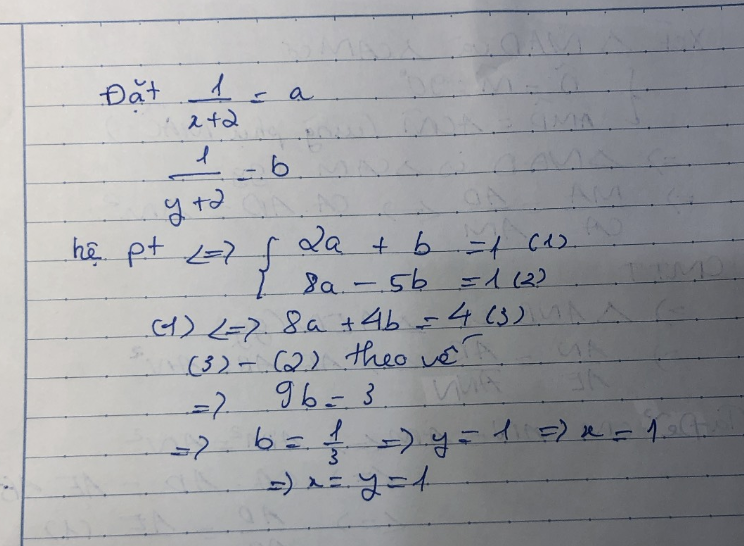


Đặt \(\dfrac{1}{x+1}\) = a; \(\dfrac{1}{y}\) = b (x \(\ne\) -1; y \(\ne\) 0)
Khi đó hpt trên tương đương:
\(\left\{{}\begin{matrix}a+b=\dfrac{-1}{2}\\8a+9b=-5\end{matrix}\right.\)
\(\Leftrightarrow\) \(\left\{{}\begin{matrix}8a+8b=-4\\8a+9b=-5\end{matrix}\right.\)
\(\Leftrightarrow\) \(\left\{{}\begin{matrix}-b=1\\8a+9b=-5\end{matrix}\right.\)
\(\Leftrightarrow\) \(\left\{{}\begin{matrix}b=-1\\8a+9\left(-1\right)=-5\end{matrix}\right.\)
\(\Leftrightarrow\) \(\left\{{}\begin{matrix}b=-1\\8a=4\end{matrix}\right.\)
\(\Leftrightarrow\) \(\left\{{}\begin{matrix}b=-1\\a=\dfrac{1}{2}\end{matrix}\right.\)
\(\Leftrightarrow\) \(\left\{{}\begin{matrix}\dfrac{1}{x+1}=\dfrac{1}{2}\\\dfrac{1}{y}=-1\end{matrix}\right.\)
\(\Leftrightarrow\) \(\left\{{}\begin{matrix}x+1=2\\y=-1\end{matrix}\right.\)
\(\Leftrightarrow\) \(\left\{{}\begin{matrix}x=1\\y=-1\end{matrix}\right.\) (TM)
Vậy hpt có nghiệm duy nhất (x; y) = (1; -1)
Chúc bn học tốt!
ĐK: ( x ≠ 1 ; y ≠ 0 )
Đặt a = \(\dfrac{1}{x+1} \) ; b = \(\dfrac{1}{y}\) . Ta có hệ phương trình
\(\begin{cases} a + b = \dfrac{-1}{2}\\ 8a + 9b = -5 \end{cases} \)
⇔\(\begin{cases} 8a + 8b = -4 \\ 8a + 9b = -5 \end{cases} \) ⇔ \(\begin{cases} -b = 1 \\ a + b = \dfrac{-1}{2} \end{cases} \) ⇔ \(\begin{cases} b = - 1 \\ a = \dfrac{1}{2} \end{cases} \)
=> \(\begin{cases} \dfrac{1}{y}=-1 \\\dfrac{1}{x+1}= \dfrac{1}{2} \end{cases} \) ⇔ \(\begin{cases} y = - 1\\ x = 1 \end{cases} \)
Vậy hpt có nghiệm duy nhất \(\begin{cases} y = - 1\\ x = 1 \end{cases} \)