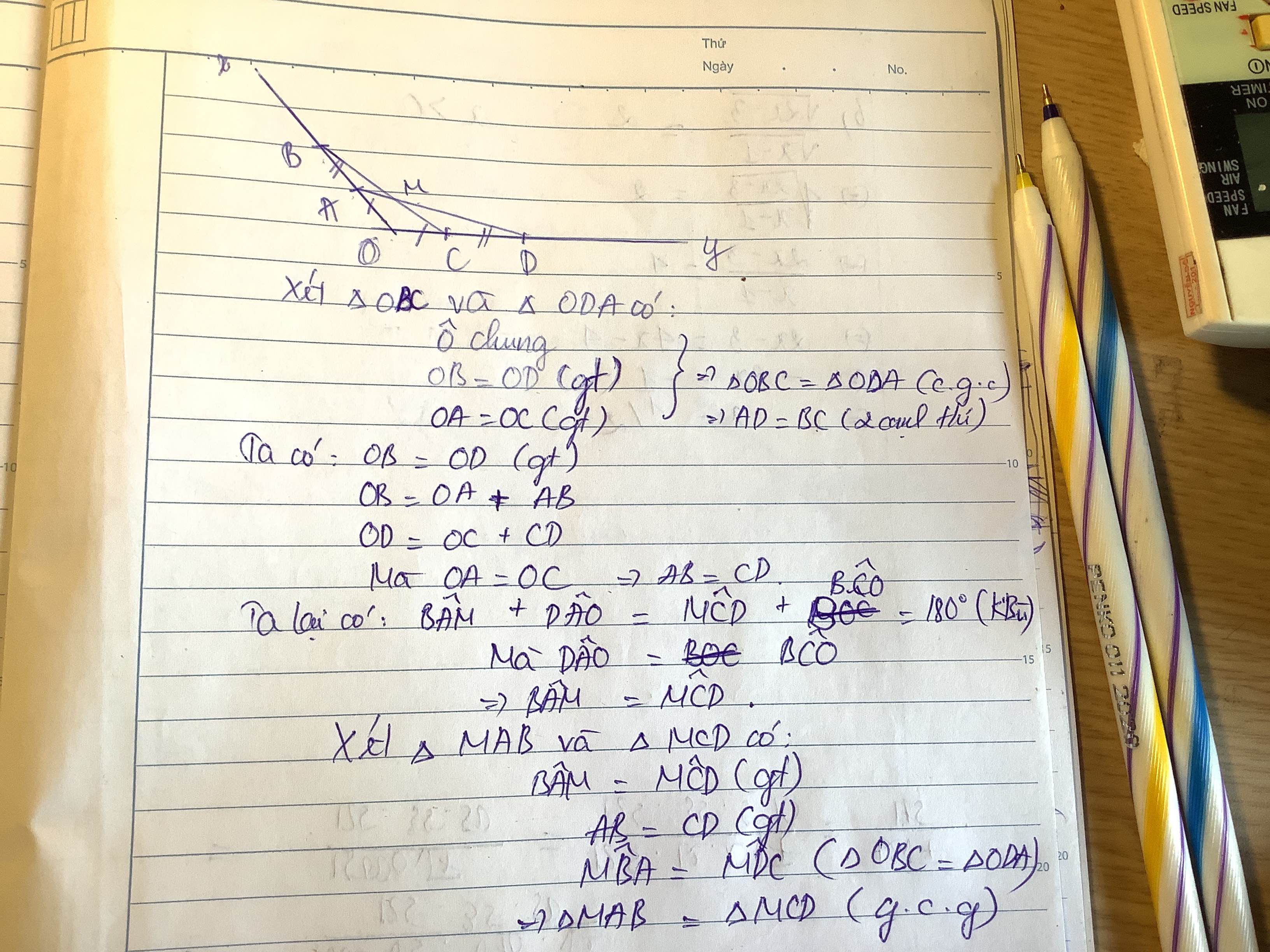Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

Xét ΔODB có
\(\dfrac{OA}{OB}=\dfrac{OC}{OD}\)
Do đó: AC//BD

a) Xét tg OBC và tg ODA
góc O chung
OB= OD ( giả thiết) (*)
OC= OA (giả thiết)
=> tg OBC= tg ODA ( C-G-C)
Suy ra : AD= BC (1)
góc ABE= góc EDC (2)
góc OCB= góc OAD (3)
b) Xét tg EAB và tg ECD: góc ABE= góc EDC ( do 2) (4)
góc BAE= góc ECD [kề bù với 2 góc OCB và OAD do (3) ] (5)
Mặt khác: A nằm giữa O, B ( OA<OB) => AB= OB - OA
C nằm giữa O, D ( OC<OD) => CD= OD - OC
Mà do (*) => AB= CD (6)
Từ (4), (5) và (6) suy ra: tg AEB= tg CED (G-C-G)
c) tg AEB= tg CED => AE= CE
mà OA= OC
OE chung của 2 tam giác
Suy ra tg OAE= tg OCE (C-C-C) (**) => góc AOE = góc COA
Do AD cắt BC(giả thiết) tại E nằm trong góc xOy => Tia OE nằm giữa 2 tia OB, OD (***)
Từ (**) và (***) suy ra: OE là tia phân giác của góc xOy.
Hết. Chúc bạn học tốt

thiếu trên tia Ox lấy điểm A,B (OA>OB)
Giúp mik vs!!!

tu ve hinh :
a, xet tamgiac OCB va tamgiac OCA co : OC chung
goc OBC = goc OAC = 90 do BC | Oy va AC | Ox (GT)
OB = OA (gt)
=> tamgiac OCB = tamgiac OCA (ch - cgv)
=> goc BOC = goc AOC (dn) ma OC nam giac Ox va Oy
=> OC la phan giac cua goc xOy (dn)
b, xet tamgiac OBD va tamgiac OAE co : OB = OA (gt)
goc BOD = goc AOE (doi dinh)
goc OBD = goc OAE = 90 do BC | Oy va AC | Ox (GT)
=> tamgiac OBD = tamgiac OAE (cgv - gnk)
=> OD = OE (dn)
=> tamgiac ODE can tai O (dn)
c, tu nghi di cau c-g-c

a: Xét ΔOAD và ΔOCB có
OA=OC
\(\widehat{COB}\) chung
OD=OB
Do đó: ΔOAD=ΔOCB
Suy ra: AD=BC
b: Ta có: ΔOAD=ΔOCB
nên \(\widehat{OAD}=\widehat{OCB}\)
mà \(\widehat{MAB}=180^0-\widehat{OAD}\)
và \(\widehat{MCD}=180^0-\widehat{OCB}\)
nên \(\widehat{MAB}=\widehat{MCD}\)
Xét ΔMAB và ΔMCD có
\(\widehat{MAB}=\widehat{MCD}\)
AB=CD
\(\widehat{MBA}=\widehat{MDC}\)
Do đó: ΔMAB=ΔMCD

Giải:
a) Xét \(\Delta OAD,\Delta OCB\) có:
\(OA=OC\left(gt\right)\)
\(\widehat{O}\): góc chung
\(OD=OB\left(gt\right)\)
\(\Rightarrow\Delta OAD=\Delta OCB\left(c-g-c\right)\)
\(\Rightarrow AD=CB\) ( cạnh t/ứng )
\(\Rightarrow\widehat{B_1}=\widehat{D_1}\) ( góc t/ứng )
b) Ta có: OB = OD
OA = OC
\(\Rightarrow OB-OA=OD-OC\)
\(\Rightarrow AB=CD\)
Ta có: \(\widehat{A_1}+\widehat{B_1}+\widehat{E_1}=180^o\)
\(\widehat{C_1}+\widehat{E_2}+\widehat{D_1}=180^o\)
Mà \(\widehat{B_1}=\widehat{D_1}\) ( theo phần a ); \(\widehat{E_1}=\widehat{E_2}\) ( đối đỉnh )
\(\Rightarrow\widehat{A_1}=\widehat{C_1}\)
Xét \(\Delta EAB,\Delta ECD\) có:
\(\widehat{A_1}=\widehat{C_1}\left(cmt\right)\)
AB = CB ( cmt )
\(\widehat{B_1}=\widehat{D_1}\) ( theo phần a )
\(\Rightarrow\Delta EAB=\Delta ECD\left(g-c-g\right)\)
\(\Rightarrow EB=ED\) ( cạnh t/ứng )
c) Xét \(\Delta OBE,\Delta ODE\) có:
\(EB=ED\) ( theo phần b )
\(\widehat{B_1}=\widehat{D_1}\) ( theo phần a )
\(OB=OD\left(gt\right)\)
\(\Rightarrow\Delta OBE=\Delta ODE\left(c-g-c\right)\)
\(\Rightarrow\widehat{O_1}=\widehat{O_2}\)
\(\Rightarrow OE\) là tia phân giác của \(\widehat{xOy}\)
Vậy...

Giải:
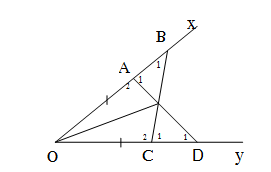
a) ∆OAD và ∆OCB có:
OA= OC(gt)
∠O chung OB = OD (gt)
OAD = OCB (c.g.c) AD = BC
Nên ∆OAD=∆OCB (c.g.c) => AD=BC.
b) Ta có
∠A1 = 1800 – ∠A2
∠C1 = 1800 – ∠C2
∠A2 = ∠C2 do ΔOAD = ΔOCB (c/m trên)
⇒ ∠A1 = ∠C1
Ta có:
OB = OA + AB
OD = OC + CD
mà OB = OD, OA = OC
⇒ AB = CD
Xét ΔEAB = ΔECD có:
∠A1 = ∠C1 (c/m trên)
AB = CD (c/m trên)
∠B1 = ∠D1 (ΔOCB = ΔOAD)
⇒ ΔEAB = ΔECD (g.c.g)
c) Xét ΔOBE và ΔODE có:
OB = OD (GT)
OE chung
AE = CE (ΔAEB = ΔCED)
⇒ΔOBE = ΔODE (c.c.c)
⇒ ∠AOE = ∠COE
⇒ OE là phân giác của góc ∠xOy.