Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

Bài 2: Tính tích của các đơn thức sau, rồi tìm bậc của đơn thức thu được:
a) 2x2y và – 11xy4 ; b) x3y2 và xy5z7

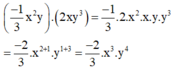
Bậc của đơn thức trên là tổng số mũ của các biến x và y
Số mũ của biến x là 3 ; số mũ của biến y là 4
⇒ Bậc của đơn thức đó là 3+4=7.


Bậc của đơn thức trên là tổng số mũ của các biến x và y
Số mũ của biến x là 6 ; số mũ của biến y là 6.
⇒ Bậc của đơn thức đó là 6+6 = 12
Tính tích các đơn thức sau rồi tìm bậc của đơn thức thu được:
a) -1/3x2y và 2xy3;
b) 1/4x3y và -2x3y5.

a,(-1/3)x2y.2xy3
=(-1/3).3.2.2.xy
=-1.4.xy
=-4xy
b,1/4xy3.(-2)x3y5
=1/4.(-2).5.3.3.xy
=1/4.-10.9xy
=-5/2.9xy
=-45/2xy

\(2,\\ a,=-3x^3y^3z^4\\ b,=\dfrac{1}{4}xy^2\cdot\dfrac{1}{4}x^4y^4\cdot\left(-\dfrac{4}{5}yz^2\right)=-\dfrac{1}{20}x^5y^7z^2\\ c,=-\dfrac{15}{14}x^6y^{11}z^{10}\\ 3,\\ a,=9\left(-1\right)\left(-\dfrac{1}{27}\right)=\dfrac{1}{3}\\ b,=-\dfrac{1}{5}\left(-8\right)=\dfrac{8}{5}\\ c,=\dfrac{4}{9}a\cdot36\left(-1\right)=-16a\)

Bài 7
\(-3y\left(x^2y^2\right)\left(-x^3y^9\right)=3x^5y^{12}\)
hệ sô : 3 ; biến x^5y^12 ; bậc 17

1/6x(2y3)2.(-9.x5y)
= 1/6.x.4y6.(-9).x5.y
= [1/6.4.(-9)].(x.x5).(y6.y)
= -6.x6.y7
Đơn thức có bậc 6 + 7 = 13.

Tích của hai đơn thức là:
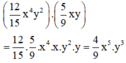
Bậc của đơn thức trên là tổng số mũ của các biến x và y
Số mũ của x là 5 ; Số mũ của y là 3
⇒ Bậc của đơn thức đó là 5+3=8.
có mũ ko đấy :v?
\(a.\left(2x^2y\right).\left(-11xy^4\right)=-22x^3y^5\)
bậc là: 8
\(b.\left(x^3y^2\right).\left(xy^5z^7\right)=x^4y^7z^7\)
bậc là: 18