Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

Gọi số sản phẩm nhóm thợ theo kế hoạch phải làm mỗi ngày là x (x ∈ ℕ * )
+) Theo kế hoạch: Thời gian hoàn thành là 3000/x (ngày)
+) Thực tế:
Số sản phẩm làm trong 8 ngày là 8x (sản phẩm)
Số sản phẩm còn lại là 3000 – 8x (sản phẩm)
Mỗi ngày sau đó nhóm thợ làm được x + 10 (sản phẩm)
Thời gian hoàn thành 3000 - 8 x x + 10 (ngày)
Vì thời gian thực tế ít hơn thời gian dự định là 2 ngày nên ta có phương trình:
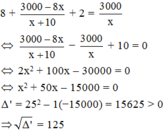
Phương trình có hai nghiệm phân biệt: x 1 = − 25 – 125 = −150 (loại) và
x 2 = −25 + 125 = 100 (tmđk)
Vậy theo kế hoạch, mỗi ngày cần làm 100 sản phẩm
Đáp án: A

Gọi khối lượng công việc mỗi ngày là x(sp)
Thời gian dự kiến là 1200/x
Thời gian thựctế là \(12+\dfrac{1200-12x}{x+20}\)
Theo đề, ta có: \(\dfrac{1200}{x}-12-\dfrac{1200-12x}{x+20}=2\)
=>\(\dfrac{1200}{x}-\dfrac{1200-12x}{x+20}=14\)
=>\(\dfrac{1200x+24000-1200x+12x^2}{x\left(x+20\right)}=14\)
=>14(x^2+20x)=24000+12x^2
=>2x^2+280x-24000=0
=>x=60

gọi x là số sản phẩm làm 1 ngày theo dự định
3200/x là số ngày làm 3200 sp theo dự định
5+(3200-5x)/(x+40) là số ngày làm xong sản phẩm thực tê
ta có pt
3200/x-3=(5+(3200-5x)/(x+40))

Gọi số sản phẩm làm theo kế hoạch mỗi ngày là x>0 và số ngày dự định là y>0
Ta có: \(xy=200\)
4 ngày đầu làm được: \(4x\) sản phẩm
Những ngày còn lại: \(\left(y-6\right)\left(x+10\right)\)
Theo bài ra ta có hệ:
\(\left\{{}\begin{matrix}xy=200\\4x+\left(y-6\right)\left(x+10\right)=200\end{matrix}\right.\)
\(\Leftrightarrow\left\{{}\begin{matrix}xy=200\\5y-x=30\end{matrix}\right.\)
\(\Rightarrow y\left(5y-30\right)=200\)
\(\Leftrightarrow y^2-6y-40=0\Rightarrow\left[{}\begin{matrix}y=10\\y=-4\left(loại\right)\end{matrix}\right.\)
\(\Rightarrow x=\dfrac{200}{10}=20\)
