Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

A = 1^2 + 3^2 + ... + 97^2 + 99^2
= 1.1 + 3.3 + ... + 97.97 + 99.99
> 1.2 + 2.3 + ... + 97.98 + 98.99
= 1.99 = 99
Suy ra A > 1

a, Ta có
\(\left|x-1,7\right|=2,3\\ \Rightarrow\left[{}\begin{matrix}x-1,7=2.3\\x-1.7=-2,3\end{matrix}\right.\Rightarrow\left[{}\begin{matrix}x=4\\x=-0,6\end{matrix}\right.\)
Vậy....
b, Ta có :
\(\left|x+\dfrac{3}{4}\right|-\dfrac{1}{3}=0\\ \Rightarrow\left|x+\dfrac{3}{4}\right|=\dfrac{1}{3}\\ \Rightarrow\left[{}\begin{matrix}x+\dfrac{3}{4}=\dfrac{1}{3}\\x+\dfrac{3}{4}=-\dfrac{1}{3}\end{matrix}\right.\Rightarrow\left[{}\begin{matrix}x=-\dfrac{5}{12}\\x=-\dfrac{13}{12}\end{matrix}\right.\)
Vậy...

f(x)=9x3-1/3x+3x2-3x+1/3x2-1/9x3-3x2-9x+27+3x
= 9x3-1/9x3+3x2+1/3x2-3x2-1/3-3x-9x+3x+27
= 80/9x3+1/3x2-28/3x+27

Từ 2x=3y=4z \(\Rightarrow\)\(\frac{x}{6}\)=\(\frac{y}{4}\)=\(\frac{z}{3}\) áp dụng tính chất dãy tỉ số bằng nhau, ta được:
\(\frac{x}{6}\) =\(\frac{y}{4}\)=\(\frac{z}{3}\)= \(\frac{y-x+z}{4-6+3}\)=\(\frac{2013}{1}\)= 2013
\(\Rightarrow\)x=2013.6=12078
\(\Rightarrow\)y= 2013.4=8052
\(\Rightarrow\)z=2013.3=6039
Vậy: x=12078
y=8052
z=6039
HOK TỐT!
@LOANPHAN.

Ta có: \(x=\frac{a+7}{a}=1+\frac{7}{a}\)
Để \(x \in Z\) thì \(1+\frac{7}{a}\in Z\)
\(\iff \frac{7}{a} \in Z\)(Vì 1 thuộc Z)
\(\iff 7\vdots a \)
\(\implies a \in Ư(7)=\{-7;-1;1;7\}\)
Vậy \(x\in Z \iff x \in \{-7;-1;1;7\}\)
_Học tốt_
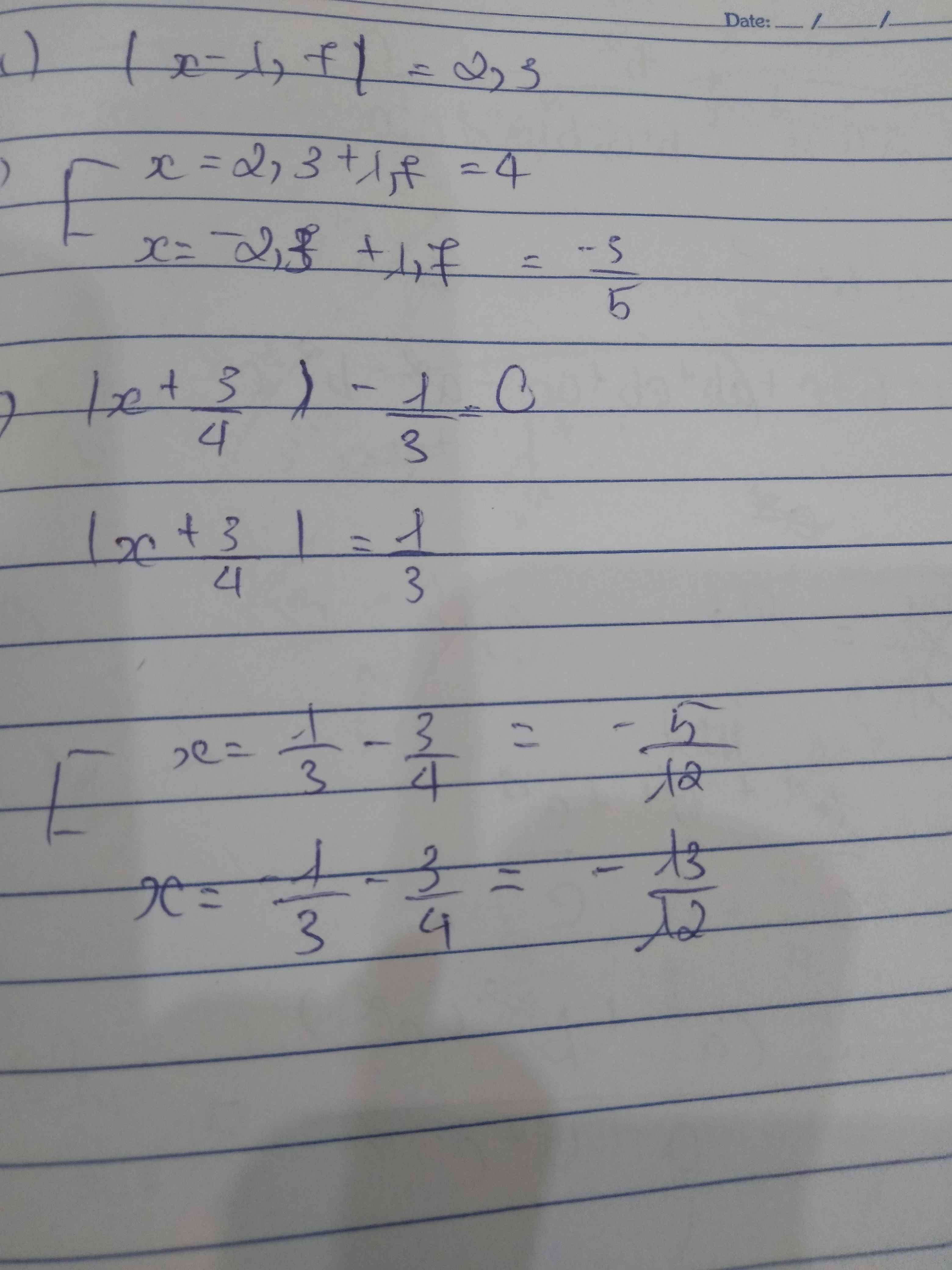
a) Xét từng vế ta có :
\(24^{54}.54^{24}.2^{10}=\left(2^3.3\right)^{54}.\left(2.3^2\right)^{24}.2^{10}\)
\(=2^{162}.3^{54}.2^{24}.3^{48}.2^{10}\)
\(=2^{172}.3^{102}\)
Xét vế tiếp theo ta có :
\(72^{63}=\left(2^3.3^2\right)^{63}=2^{189}.3^{126}\)
\(\Rightarrow72^{63}⋮24^{54}.2^{10}.54^{24}\)
\(\RightarrowĐPCM\)