Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
cắt nhau tại I.
. Tính 
cắt (O) tại điểm thứ hai là K (K
. Vẽ đường kính CD của (O). Gọi P là trung điểm của AB. Chứng minh: K, P, D thẳng hàng.
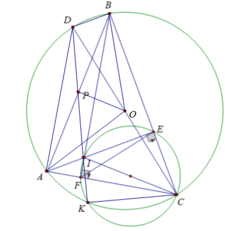
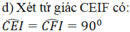
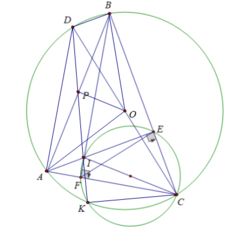
⇒ Tứ giác CEIF là tứ giác nội tiếp và CI là đường kính đường tròn ngoại tiếp tứ giác CEIF
Ta có: IK ⊥ KC ( góc nội tiếp chắn nửa đường tròn ngoại tiếp tứ giác CEIF)
DK ⊥ KC (góc nội tiếp chắn nửa đường tròn (O)
⇒ D; I; K thẳng hàng (1)
Ta có:
DB ⊥ BC (góc nội tiếp chắn nửa đường tròn (O)
AI ⊥ BC ( AI là đường cao của tam giác ABC)
⇒ AI // BD
DA ⊥ BA(góc nội tiếp chắn nửa đường tròn (O)
BI ⊥ BA ( BI là đường cao của tam giác ABC)
⇒ AD // BI
Xét tứ giác ADBI có: AI // BD và AD // BI
⇒ ADBI là hình bình hành
Do P là trung điểm của AB ⇒ P là trung điểm của DI
Hay D; P; I thẳng hàng (2)
Từ (1) và (2) ⇒ D; P; K thẳng hàng.
a) Xét tứ giác AEFB có:
∠(AFB) = 90 0 ( AF là đường cao)
∠(AEB) = 90 0 ( BE là đường cao)
⇒ 2 đỉnh E và F cùng nhìn cạnh AB dưới 1 góc bằng nhau
⇒ AEFB là tứ giác nội tiếp.
a, HS tự chứng minh
b, Chứng minh ∆NMC:∆NDA và ∆NME:∆NHA
c, Chứng minh ∆ANB có E là trực tâm => AE ⊥ BN mà có AK ⊥ BN nên có ĐPCM
Chứng minh tứ giác EKBH nội tiếp, từ đó có A K F ^ = A B M ^
d, Lấy P và G lần lượt là trung điểm của AC và OP
Chứng minh I thuộc đường tròn (G, GA)
4]
tg DEC ~ tg DCB
=> EC/BC = DC/DB
=> EC = BC.DC/DB
=> AC.EC = AC.BC.DC/DB = 2S(ACB).DC/DB
Cần c/m AF.CH = AC.EC
<=> AF.CH = 2S(ACB).DC/DB
<=> AE.DB = 2S(ACB).DC/CH (*)
Mà 2S(ACB)/CH = AB
=> (*) <=> AE.DB = AB.DC = AB.DA
Mà AE.DB = 2S(ADB); AB.DA = 2S(ADB)
Vậy: AF.CH = AC.EC
5]
Ta đi c/m KA=KD để suy ra KE là tiếp tuyến.
AE kéo dài CH tại M
=> AK/CM = KI/IC
=> KD/CH = KI/IC
=> AK/CM = KD/CH (*)
DP cắt CH tại P; BC cắt AD tại J
=> HP/AD = BP/BD = CP/DJ (**)
Tam giác ACJ vuông tại C, AD=AD => DC là trung tuyến => AD=DJ
Từ (**) => HP=PC
Xét 2 tg vuông AMH và HBP, ta có ^AMH = ^HBP (cạnh tương ứng vuông góc)
=> tg AMH ~ HBP
=> MH/AH = HB/PH
=> MH = AH.HB/PH = AH.HB/(CH/2) = 2AH.HB/CH (***)
Do CH^2 = AH.HB => AH.HB/CH = CH
Từ (***) => MH = 2CH => CM =CH
Từ (*) => AK =KD
=> KE là trung tuyến tg vuông ADE => ka=ke
=> tg OKA = tg OKE (do OA=OE, OK chung; AK=KD)
=> ^KEO = ^KAO = 90
=> KE là tiếp tuyến của (O)
