Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

Bài 1 :
a, \(A=\frac{2x^2-4x+8}{x^3+8}=\frac{2\left(x^2-2x+4\right)}{\left(x+2\right)\left(x^2-2x+4\right)}=\frac{2}{x+2}\)
b, Ta có : \(\left|x\right|=2\Rightarrow\orbr{\begin{cases}x=2\\x=-2\end{cases}}\)
TH1 : Thay x = 2 vào biểu thức trên ta được :
\(\frac{2}{2+2}=\frac{2}{4}=\frac{1}{2}\)
TH2 : Thay x = -2 vào biểu thức trên ta được :
\(\frac{2}{-2+2}=\frac{2}{0}\)vô lí
c, ta có A = 2 hay \(\frac{2}{x+2}=2\)ĐK : \(x\ne-2\)
\(\Rightarrow2x+4=2\Leftrightarrow2x=-2\Leftrightarrow x=-1\)
Vậy với x = -1 thì A = 2
d, Ta có A < 0 hay \(\frac{2}{x+2}< 0\)
\(\Rightarrow x+2< 0\)do 2 > 0
\(\Leftrightarrow x< -2\)
Vậy với A < 0 thì x < -2
e, Để A nhận giá trị nguyên khi \(x+2\inƯ\left(2\right)=\left\{\pm1;\pm2\right\}\)
| x + 2 | 1 | -1 | 2 | -2 |
| x | -1 | -3 | 0 | -4 |
2.
ĐKXĐ : \(x\ne\pm2\)
a. \(B=\frac{x^2-4x+4}{x^2-4}=\frac{\left(x-2\right)^2}{\left(x-2\right)\left(x+2\right)}=\frac{x-2}{x+2}\)
b. | x - 1 | = 2 <=>\(\hept{\begin{cases}x-1=2\\x-1=-2\end{cases}}\)<=>\(\hept{\begin{cases}x=3\\x=-1\end{cases}}\)
Với x = 3 thì \(B=\frac{3-2}{3+2}=\frac{1}{5}\)
Với x = - 1 thì \(B=\frac{-1-2}{-1+2}=-3\)
Vậy với | x - 1 | = 2 thì B đạt được 2 giá trị là B = 1/5 hoặc B = - 3
c. \(B=\frac{x-2}{x+2}=-1\)<=>\(-\left(x-2\right)=x+2\)
<=> \(-x+2=x+2\)<=>\(-x=x\)<=>\(x=0\)
d. \(B=\frac{x-2}{x+2}< 1\)<=>\(x-2< x+2\)luôn đúng \(\forall\)x\(\ne\pm2\)
e. \(B=\frac{x-2}{x+2}=\frac{x+2-4}{x+2}=1-\frac{4}{x+2}\)
Để B nguyên thì 4/x+2 nguyên => x + 2\(\in\){ - 4 ; - 2 ; - 1 ; 1 ; 2 ; 4 }
=> x \(\in\){ - 6 ; - 4 ; - 3 ; - 1 ; 0 ; 2 }

Điều kiện x ≠ 2 và x ≠ 0
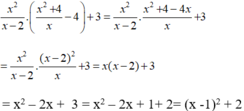
Vì x - 1 2 ≥ 0 nên x - 1 2 + 2 ≥ 2 với mọi giá trị của x.
Khi đó giá trị nhỏ nhất của biểu thức bằng 2 khi x = 1.
Vậy biểu thức đã cho có giá trị nhỏ nhất bằng 2 tại x = 1.

a) Giá trị của phân thức M được xác định khi:
\(x^2+2x-8\ne0\)
\(\Leftrightarrow\left(x^2+2x+1\right)-9\ne0\)
\(\Leftrightarrow\left(x+1\right)^2-9\ne0\)
\(\Leftrightarrow\left(x-2\right)\left(x+4\right)\ne0\)
\(\Rightarrow x-2\ne0\)và \(x+4\ne0\), do đó: \(x\ne2\)và \(x\ne4\)
Với: ĐK: \(x\ne2\)và \(x\ne-4\)thì giá trị của phân thức M được xác định.
P/s: Mình chỉ giải được phần a) thôi xin lỗi bạn nha!
ĐẬP A CỦA MK LÀ
NẾU ĐÚNG HÃY TÍCH CHO MK MHA
a/ giá trị phân thức M được xác ding khi
x^2 + 2x - 8 khác 0
< = > ( x^2 - 2x = 1 ) - 9 khác 0
< = >( x + 1 )^ 2 - 9 khác 0
< => ( x - 2 ) . ( x + 4 ) khac 0
=> x - 2 khác 0 và x + 4 khác 0 => x khác 2 và x khác 4
ta có ding nghĩa x khác 2 và x khác 4 thì giá trị phân thức M được xác ding
CHÚC BẠN HC TỐT NHA
xin lỗi ban nha mk chỉ giải đc phần a thôi

a. \(A=\dfrac{1}{x-1}-\dfrac{1}{x+1}+\dfrac{4x+2}{x^2-1}\)
\(A=\dfrac{x+1}{\left(x-1\right)\left(x+1\right)}-\dfrac{x-1}{\left(x-1\right)\left(x+1\right)}+\dfrac{4x+2}{\left(x-1\right)\left(x+1\right)}\)
\(A=\dfrac{\left(x+1\right)-\left(x-1\right)+4x+2}{\left(x-1\right)\left(x+1\right)}\)
\(A=\dfrac{x+1-x+1+4x+2}{\left(x-1\right)\left(x+1\right)}\)
\(A=\dfrac{4x+4}{\left(x-1\right)\left(x+1\right)}=\dfrac{4\left(x+1\right)}{\left(x-1\right)\left(x+1\right)}=\dfrac{4}{x-1}\)
b) Ta có: \(A=\dfrac{4}{x-1}=\dfrac{4}{2015}\) (ĐK: \(x\ne\pm1\) )
\(\Leftrightarrow8060=4\left(x-1\right)\)
\(\Leftrightarrow8060=4x-4\)
\(\Leftrightarrow8064=4x\)
\(\Leftrightarrow x=\dfrac{8064}{4}=2016\left(tm\right)\)
c) Ta có: \(\dfrac{4}{x-1}\left(x\ne1\right)\)
Để \(\dfrac{4}{x-1}\) nhận giá trị nguyên thì \(4:\left(x-1\right)\Leftrightarrow x-1\in\text{Ư}\left(4\right)=\left\{1;4;2\right\}\)
Vậy với x ∈ {2; 5; 3; 0; -1; -3} thì biểu thức \(\dfrac{4}{x-1}\) nhận giá trị nguyên
d) Thay \(x=-\dfrac{1}{2}\) vào biểu thức A ta được:
\(\dfrac{4}{-\dfrac{1}{2}-1}=-3\)
Vậy biểu thức A có giá trị -3 tại \(x=-\dfrac{1}{2}\)

a)
\(ĐKXĐ:\left\{{}\begin{matrix}x-2\ne0\\x+2\ne0\\x^2-4\ne0\end{matrix}\right.< =>\left\{{}\begin{matrix}x\ne2\\x\ne-2\end{matrix}\right.\)
b)
\(\dfrac{1}{x-2}-\dfrac{1}{x+2}+\dfrac{x^2+4x}{x^2-4}\)
\(=\dfrac{1}{x-2}-\dfrac{1}{x+2}+\dfrac{x\left(x+4\right)}{\left(x-2\right)\left(x+2\right)}\)
\(=\dfrac{x+2}{\left(x-2\right)\left(x+2\right)}-\dfrac{x-2}{\left(x-2\right)\left(x+2\right)}+\dfrac{x\left(x+4\right)}{\left(x-2\right)\left(x+2\right)}\)
\(=\dfrac{x+2-x+2+x^2+4x}{\left(x-2\right)\left(x+2\right)}\)
\(=\dfrac{x^2+4x+4}{\left(x-2\right)\left(x+2\right)}\\ =\dfrac{\left(x+2\right)^2}{\left(x-2\right)\left(x+2\right)}\\ =\dfrac{x+2}{x-2}\)
c)
\(\dfrac{x+2}{x-2}=\dfrac{x-2+4}{x-2}=\dfrac{x-2}{x-2}+\dfrac{4}{x-2}=1+\dfrac{4}{x-2}\)
vậy M nhận giá trị nguyên thì 4⋮x-2
=> x-2 thuộc ước của 4
\(Ư\left(4\right)\in\left\{-1;1;-2;2;;4;-4\right\}\)
ta có bảng sau
| x-2 | -1 | 1 | -2 | 2 | 4 | -4 |
| x | 1(tm) | 3(tm) | 0(tm) | 4(tm) | 6(tm | -2(loại) |

Bài 1:
a) Ta có: \(P=1+\dfrac{3}{x^2+5x+6}:\left(\dfrac{8x^2}{4x^3-8x^2}-\dfrac{3x}{3x^2-12}-\dfrac{1}{x+2}\right)\)
\(=1+\dfrac{3}{\left(x+2\right)\left(x+3\right)}:\left(\dfrac{8x^2}{4x^2\left(x-2\right)}-\dfrac{3x}{3\left(x-2\right)\left(x+2\right)}-\dfrac{1}{x+2}\right)\)
\(=1+\dfrac{3}{\left(x+2\right)\left(x+3\right)}:\left(\dfrac{4}{x-2}-\dfrac{x}{\left(x-2\right)\left(x+2\right)}-\dfrac{1}{x+2}\right)\)
\(=1+\dfrac{3}{\left(x+2\right)\left(x+3\right)}:\dfrac{4\left(x+2\right)-x-\left(x-2\right)}{\left(x-2\right)\left(x+2\right)}\)
\(=1+\dfrac{3}{\left(x+2\right)\left(x+3\right)}\cdot\dfrac{\left(x-2\right)\left(x+2\right)}{4x+8-x-x+2}\)
\(=1+3\cdot\dfrac{\left(x-2\right)}{\left(x+3\right)\left(2x+10\right)}\)
\(=1+\dfrac{3\left(x-2\right)}{\left(x+3\right)\left(2x+10\right)}\)
\(=\dfrac{\left(x+3\right)\left(2x+10\right)+3\left(x-2\right)}{\left(x+3\right)\left(2x+10\right)}\)
\(=\dfrac{2x^2+10x+6x+30+3x-6}{\left(x+3\right)\left(2x+10\right)}\)
\(=\dfrac{2x^2+19x-6}{\left(x+3\right)\left(2x+10\right)}\)

\(a,M=x^2-64+x^3+64=x^3+x^2\\ b,x=-4\Leftrightarrow M=-64+16=-48\\ c,M=0\Leftrightarrow x^2\left(x+1\right)=0\Leftrightarrow\left[{}\begin{matrix}x=0\\x=-1\end{matrix}\right.\)