Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

a) x = -1. b) x = 4 hoặc x = 5.
c) x = ± 2 . d) x = 1 hoặc x = 2.

a) \(\Rightarrow x\left(x+3\right)=0\)
\(\Rightarrow\left[{}\begin{matrix}x=0\\x=-3\end{matrix}\right.\)
b) \(\Rightarrow x\left(x^2-4\right)=0\Rightarrow x\left(x-2\right)\left(x+2\right)=0\)
\(\Rightarrow\left[{}\begin{matrix}x=0\\x=2\\x=-2\end{matrix}\right.\)
c) \(\Rightarrow\left(x-1\right)\left(5x-1\right)=0\)
\(\Rightarrow\left[{}\begin{matrix}x=1\\x=\dfrac{1}{5}\end{matrix}\right.\)
d) \(\Rightarrow2\left(x+5\right)-x\left(x+5\right)=0\Rightarrow\left(x+5\right)\left(2-x\right)=0\)
\(\Rightarrow\left[{}\begin{matrix}x=-5\\x=2\end{matrix}\right.\)
e) \(\Rightarrow2x^2-10x-3x-2x^2=26\)
\(\Rightarrow-13x=26\Rightarrow x=-2\)
f) \(\Rightarrow\left(x-2012\right)\left(5x-1\right)=0\)
\(\Rightarrow\left[{}\begin{matrix}x=2012\\x=\dfrac{1}{5}\end{matrix}\right.\)

Bài 1:
a) (3x - 2)(4x + 5) = 0
<=> 3x - 2 = 0 hoặc 4x + 5 = 0
<=> 3x = 2 hoặc 4x = -5
<=> x = 2/3 hoặc x = -5/4
b) (2,3x - 6,9)(0,1x + 2) = 0
<=> 2,3x - 6,9 = 0 hoặc 0,1x + 2 = 0
<=> 2,3x = 6,9 hoặc 0,1x = -2
<=> x = 3 hoặc x = -20
c) (4x + 2)(x^2 + 1) = 0
<=> 4x + 2 = 0 hoặc x^2 + 1 # 0
<=> 4x = -2
<=> x = -2/4 = -1/2
d) (2x + 7)(x - 5)(5x + 1) = 0
<=> 2x + 7 = 0 hoặc x - 5 = 0 hoặc 5x + 1 = 0
<=> 2x = -7 hoặc x = 5 hoặc 5x = -1
<=> x = -7/2 hoặc x = 5 hoặc x = -1/5

Bài 1
a/ \(x\left(x^2+1\right)+2\left(x^2+1\right)=0\)
\(\Leftrightarrow\left(x+2\right)\left(x^2+1\right)=0\Rightarrow x=-2\)
b/
\(\Leftrightarrow x^3-6x^2+9x+5x^2-30x+45=0\)
\(\Leftrightarrow x\left(x-3\right)^2+5\left(x-3\right)^2=0\)
\(\Leftrightarrow\left(x+5\right)\left(x-3\right)^2=0\)
\(\Rightarrow\left[{}\begin{matrix}x=-5\\x=3\end{matrix}\right.\)
1.
c/ \(\Leftrightarrow x^3+2x^2+2x+x^2+2x+2=0\)
\(\Leftrightarrow x\left(x^2+2x+2\right)+x^2+2x+2=0\)
\(\Leftrightarrow\left(x+1\right)\left(x^2+2x+2\right)=0\)
\(\Leftrightarrow\left[{}\begin{matrix}x=-1\\x^2+2x+2=0\left(vn\right)\end{matrix}\right.\)
d/
\(\Leftrightarrow x^4+x^3-2x^2-x^3-x^2+2x+4x^2+4x-8=0\)
\(\Leftrightarrow x^2\left(x^2+x-2\right)-x\left(x^2+x-2\right)+4\left(x^2+x-2\right)=0\)
\(\Leftrightarrow\left(x^2-x+4\right)\left(x^2+x-2\right)=0\)
\(\Leftrightarrow\left[{}\begin{matrix}x^2-x+4=0\left(vn\right)\\x^2+x-2=0\end{matrix}\right.\)
\(\Rightarrow\left[{}\begin{matrix}x=1\\x=-2\end{matrix}\right.\)

a: ĐKXĐ của A là x<>1; x<>-3
ĐKXĐ của B là x<>4
ĐKXĐ của C là x<>0; x<>2
ĐKXĐ của D là x<>3
ĐKXĐ của E là x<>0; x<>2
b: \(A=\dfrac{2x\left(x+3\right)}{\left(x-1\right)\left(x+3\right)}=\dfrac{2x}{x-1}\)
Để A=0 thì 2x=0
=>x=0
\(B=\dfrac{\left(x-4\right)\left(x+4\right)}{\left(x-4\right)^2}=\dfrac{x+4}{x-4}\)
Để B=0 thì x+4=0
=>x=-4
\(C=\dfrac{x\left(x+2\right)}{x\left(x-2\right)}=\dfrac{x+2}{x-2}\)
Để C=0 thì x+2=0
=>x=-2
\(D=\dfrac{\left(x+4\right)\left(x-3\right)}{\left(x-3\right)\left(x^2+3x+9\right)}=\dfrac{x+4}{x^2+3x+9}\)
Để D=0 thi x+4=0
=>x=-4
\(E=\dfrac{2x\left(x^2+2x+1\right)}{2x\left(x-2\right)}=\dfrac{\left(x+1\right)^2}{x-2}\)
Để E=0 thì (x+1)^2=0
=>x=-1

a: \(\Leftrightarrow x\left(x-5\right)\left(x+5\right)=0\)
\(\Leftrightarrow\left[{}\begin{matrix}x=0\\x=5\\x=-5\end{matrix}\right.\)
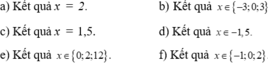
a)\(x\left(x^2-0,25\right)=0\)
TH1:\(x=0\) TH2:\(x^2-0,25=0\)
\(x^2=0,25=>x=0,5\)
Vậy x E \(\hept{0,5;0}\)