K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Các câu hỏi dưới đây có thể giống với câu hỏi trên
NV
Nguyễn Việt Lâm
Giáo viên
24 tháng 4 2022
\(d\left(G;\left(ABCD\right)\right)=\dfrac{1}{3}d\left(S;\left(ABCD\right)\right)=\dfrac{1}{3}.\dfrac{a\sqrt{3}}{2}=\dfrac{a\sqrt{3}}{6}\)
\(S_{\Delta ACD}=\dfrac{1}{2}S_{ABCD}=\dfrac{a^2}{2}\)
\(\Rightarrow V=\dfrac{1}{3}.\dfrac{a^2}{2}.\dfrac{a\sqrt{3}}{6}=\dfrac{a^3\sqrt{3}}{36}\)
DT
2
3 tháng 7 2019
Số số hạng có trong dãy là:
\(\frac{90-11}{1}+1=80\)(số hạng)
\(11+12+13+14+...+90\)
\(=\frac{\left(90+11\right)\cdot80}{2}\)
\(=4040\)
Đáp số: \(4040\)
CM
1 tháng 6 2018
Chọn D
Đường thẳng d₁ đi qua điểm M₁ = (3;-1;-1) và có một véctơ chỉ phương là 
Đường thẳng d₂ đi qua điểm M₂ = (0;0;1) và có một véctơ chỉ phương là 
Do 
và M₁ ∉ d₁ nên hai đường thẳng d₁ và d₂ song song với nhau.
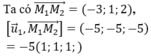
Gọi (α) là mặt phẳng chứa d₁ và d₂ khi đó (α) có một véctơ pháp tuyến là 
. Phương trình mặt phẳng (α) là x+y+z-1=0.
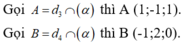
Do 
không cùng phương với 
nên đường thẳng AB cắt hai đường thẳng d₁ và d₂.
CM
7 tháng 5 2018
Chọn D
Đường thẳng d1 đi qua điểm M1 (3; -1; -1) và có một véctơ chỉ phương là 
Đường thẳng d2 đi qua điểm M2 (0; 0; 1) và có một véctơ chỉ phương là 
Do 
và M1 ∉ d1 nên hai đường thẳng d1 và d2 song song với nhau.
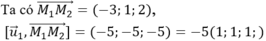
Gọi (α) là mặt phẳng chứa d1 và d2 khi đó (α) có một véctơ pháp tuyến là 
Phương trình mặt phẳng (α) là x + y + z -1 = 0
Gọi A = d3 ∩ (α) thì A (1; -1; 1)
Gọi B = d4 ∩ (α) thì B (-1; 2; 0)
Do 
không cùng phương với 
nên đường thẳng AB cắt hai đường thẳng d1 và d2.
CM
23 tháng 11 2017
Chọn A
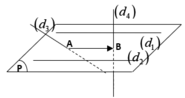
Ta có d1 song song d2, phương trình mặt phẳng chứa hai đường thẳng d1, d2 là
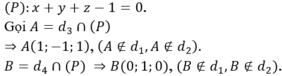
Mà 
cùng phương với véc-tơ chỉ phương của hai đường thẳng d1, d2 nên không tồn tại đường thẳng nào đồng thời cắt cả bốn đường thẳng trên.
AH
Akai Haruma
Giáo viên
24 tháng 10 2017
Câu 11:
Ta có:
\(y=x^3-3(m+1)x^2+2(m^2+4m+1)x-4m(m+1)\)
\(=x^2(x-2)-3mx(x-2)-x(x-2)+2m(x-2)+2m^2(x-2)\)
\(\Leftrightarrow y=(x-2)[x^2-x(3m+1)+2m^2+2m]\)
Ta thấy, pt \(y=0\) có bao nhiêu nghiệm thì có bấy nhiêu điểm là giao của $y$ với trục hoành.
Thấy \(x=2\) là một nghiệm của pt thỏa mãn lớn hơn 1. Vậy ta cần pt \(x^2-x(3m+1)+2m^2+2m=0\) có hai nghiệm phân biệt khác $2$ và lớn hơn 1
Trước tiên, để pt trên có hai nghiệm phân biệt khác $2$ thì:
\(\left\{\begin{matrix} 2^2-2(3m+1)+2m^2+2m\neq 0\\ \Delta=(3m+1)^2-4(2m^2+2m)>0\end{matrix}\right.\)
\(\Leftrightarrow \left\{\begin{matrix} 2(m-1)^2\neq 0\\ (m-1)^2>0\end{matrix}\right.\Leftrightarrow m\neq 1(1)\)
Theo định lý Viete, giả sử $x_1,x_2$ là hai nghiệm của pt trên thì \(\left\{\begin{matrix} x_1+x_2=3m+1\\ x_1x_2=2m^2+2m\end{matrix}\right.\)
Để pt có hai nghiệm lớn hơn 1 thì: \(\left\{\begin{matrix} (x_1-1)(x_2-1)>0\\ x_1+x_2>2 \end{matrix}\right.\Leftrightarrow \left\{\begin{matrix} 2m^2+2m-(3m+1)+1>0\\ 3m+1>2\end{matrix}\right.\)
\(\Leftrightarrow \left\{\begin{matrix} 2m^2-m=m(2m-1)>0\\ m>\frac{1}{3}\end{matrix}\right.\Leftrightarrow m>1\) hoặc \(\frac{1}{3}< m< \frac{1}{2}\)
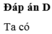
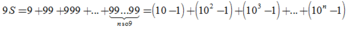
=2 nhé
bằng 2