Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

Lời giải:
Gọi $a,b$ lần lượt là vận tốc của Minh và Nam.
Khi gặp nhau lần 1 tại điểm $I$, Minh và Nam đều đi mất số thời gian như nhau, do đó: $\frac{AI}{a}=\frac{BI}{b}$
$\Leftrightarrow \frac{AB-BI}{a}=\frac{BI}{b}\Leftrightarrow \frac{7}{a}=\frac{5}{b}\Rightarrow a=\frac{7}{5}b(*)$
Khi gặp nhau lần 2 tại điểm $K$, Minh và Nam cũng đều đã mất số thời gian như nhau. Do đó:
$\frac{AB+BK}{a}=\frac{BA+AK}{b}$
$\Leftrightarrow \frac{2AB-AK}{a}=\frac{AB+AK}{b}(**)$
Từ $(*); (**)\Rightarrow AK=\frac{1}{4}AB=30$ (km)
Lời giải:
Gọi $a,b$ lần lượt là vận tốc của Minh và Nam.
Khi gặp nhau lần 1 tại điểm $I$, Minh và Nam đều đi mất số thời gian như nhau, do đó: $\frac{AI}{a}=\frac{BI}{b}$
$\Leftrightarrow \frac{AB-BI}{a}=\frac{BI}{b}\Leftrightarrow \frac{7}{a}=\frac{5}{b}\Rightarrow a=\frac{7}{5}b(*)$
Khi gặp nhau lần 2 tại điểm $K$, Minh và Nam cũng đều đã mất số thời gian như nhau. Do đó:
$\frac{AB+BK}{a}=\frac{BA+AK}{b}$
$\Leftrightarrow \frac{2AB-AK}{a}=\frac{AB+AK}{b}(**)$
Từ $(*); (**)\Rightarrow AK=\frac{1}{4}AB=30$ (km)

C đối xứng với A qua d => d là trung trực của AC
D; E thuộc d => EA = EC và DA = DC
ta có : AD + DB = DC + DB = CB
AE + EB = EC + EB
Trong tam giác BEC có: BC < EC + EB => AD + BD < AE + BE
b﴿ Giả sử bạn Tú đến điểm E bất kì trên d
ta có: Quãng đường bạn cần đi là AE + EB
mà AE + EB = CE + EB
ta luôn có: CE + EB ≥ CB
đê đi gần nhất thì CE + EB nhỏ nhất = CB
Dấu "=" xảy ra khi E trùng với D
vậy....

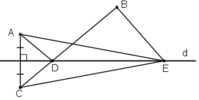
a) + A và C đối xứng qua d
⇒ d là trung trực của AC
⇒ AD = CD
⇒ AD + DB = CD + DB = CB (1)
+ E ∈ d ⇒ AE = CE
⇒ AE + EB = CE + EB (2)
+ CB < CE + EB (3)
Từ (1), (2), (3) ⇒ AD + DB < AE + EB
b) Vì với mọi E ∈ d thì AE + EB > AD + DB
Do đó con đường ngắn nhất bạn Tú nên đi là đường ADB.

Gọi a là độ dài quãng đường AB(a>0)(km)
là độ dài quãng đường AB(km)
là thời gian của xe máy đi hết quãng đường AB(h)
= là thời gian của oto đi hết nửa quãng đường đầu(h)
= là thời gian oto đi hết nửa quãng đương sau(h)
Đổi 1 giờ 10 phút = h
Lập pt:
Giải ta được a = 120
Vậy độ dài quãng đường AB là 120 km

