Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

Bài 1 Giải
Chu vi HCN là:
(12+8).2= 40(cm)
Diện tích HCN là:
12.8= 96(cm)
Bài 2 Chu vi hình vuông là:
20.4=80(cm)
Mà chu vi hình vuông bằng chu vi HCN nên:
Chiều rộng HCN là:
(80:2) -25=15(cm)
Diện tích HCN là:
15.25=375(cm)
Bài 3 Độ dài cạnh BC là:
120:10.2=24(cm)
Bài 4 Diện tích tam giác ABC là:
( 5.8):2 = 20(cm)
Chúc bn hok tốt~~

Bài 1:
Gọi chiều dài là x,gọi chiều rộng là y
Vì chiều rộng kém chiều dài 20cm ta có: x-20=y hay x-y=20 (1)
Vì chu vi hình chữ nhật là 72, ta có: (x+y).2=72 => x+y=36 (2)
Từ (1)(2) ta có:\(\begin{cases}x-y=20\\x+y=36\end{cases}\) \(\Leftrightarrow\begin{cases}x=20+y\\20+y+y=36\end{cases}\)
\(\Leftrightarrow\begin{cases}x=20+y\\2y=16\end{cases}\) \(\Leftrightarrow\begin{cases}x=20+y\\y=8\end{cases}\) \(\Leftrightarrow\begin{cases}x=28\\y=8\end{cases}\)
Diện tịhs hình chữ nhật là: x.y=28.8=224
Bài 2
Xét ΔHAB và ΔACB có:
\(\widehat{AHB}=\widehat{BAC}=90\)
\(\widehat{B}\) : góc chung
=>ΔHAB~ΔACB(g.g)
b) Xét ΔABC vuông tại A(gt)
=>\(BC^2=AB^2+AC^2\) (theo định lý pytago)
=>\(BC^2=12^2+16^2=400\)
=>BC=20cm
Vì ΔHAB~ΔACB(cmt)
=>\(\frac{AH}{AC}=\frac{AB}{BC}\)
=>\(AH=\frac{AB\cdot AC}{BC}=\frac{12\cdot16}{20}=9,6cm\)

+ BC = BH + HC = 25 + 36 = 61 (cm)
+ ΔABH vuông tại H và ΔABC vuông tại A có:
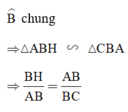
⇒AB2=BH.BC=25.(25+36)=1525


b) Áp dụng định lí Pytago vào ΔABC vuông tại A, ta được:
\(BC^2=AB^2+AC^2\)
\(\Leftrightarrow BC^2=12^2+16^2=400\)
hay BC=20(cm)
Vậy: BC=20cm

Bài 2:
a: H là trung điểm của BC
nên HB=HC=2,5(cm)
\(\Leftrightarrow AH=\dfrac{5\sqrt{15}}{2}\left(cm\right)\)
\(S=\dfrac{\dfrac{5\sqrt{15}}{2}\cdot5}{2}=\dfrac{25\sqrt{15}}{4}\left(cm^2\right)\)
b: Xét ΔABC có
M là trung điểm của AB
N là trung điểm của AC
Do đó: MN là đường trung bình của ΔABC
Suy ra: MN//BC
Xét tứ giác BMNC có MN//BC
nên BMNC là hình thang
mà \(\widehat{B}=\widehat{C}\)
nên BMNC là hình thang cân