Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

a, \(x^2-6=x^2-\sqrt{6^2}=\left(x-\sqrt{6}\right)\left(x+\sqrt{6}\right)\)
b, \(x^2+2\sqrt{3}x+3=x^2+2\sqrt{3}x+\sqrt{3}=\left(x+\sqrt{3}\right)^2=\left(x+\sqrt{3}\right)\left(x+\sqrt{3}\right)\)
c, \(x^2-2\sqrt{5}x+5=x^2-2\sqrt{5}x+\sqrt{5}=\left(x-\sqrt{5}\right)^2=\left(x-\sqrt{5}\right)\left(x-\sqrt{5}\right)\)

a) Có \(x+1< x+2\)
\(\Rightarrow\sqrt{x+1}< \sqrt{x+2}\)
\(\Leftrightarrow\frac{\sqrt{x+1}}{\sqrt{x+2}}< 1\)
b) Vì \(\sqrt{x+1}< \sqrt{x+2}\)
\(\Rightarrow\sqrt{x+1}.\sqrt{x+1}.\sqrt{x+2}< \sqrt{x+2}.\sqrt{x+1}.\sqrt{x+1}\)
\(\Leftrightarrow\sqrt{x+1}^2.\sqrt{x+2}< \sqrt{x+2}^2.\sqrt{x+1}\)
\(\Rightarrow\frac{\sqrt{x+1}^2}{\sqrt{x+2}^2}< \frac{\sqrt{x+1}}{\sqrt{x+2}}\)
hay \(\frac{\sqrt{x+1}}{\sqrt{x+2}}>\frac{\sqrt{x+1}^2}{\sqrt{x+2}^2}\)


Bạn cần viết lại đề bằng công thức toán (gõ công thức trong hộp có biểu tượng $\sum$) để được hỗ trợ tốt hơn. Nhìn đề thế này rối mắt quá.
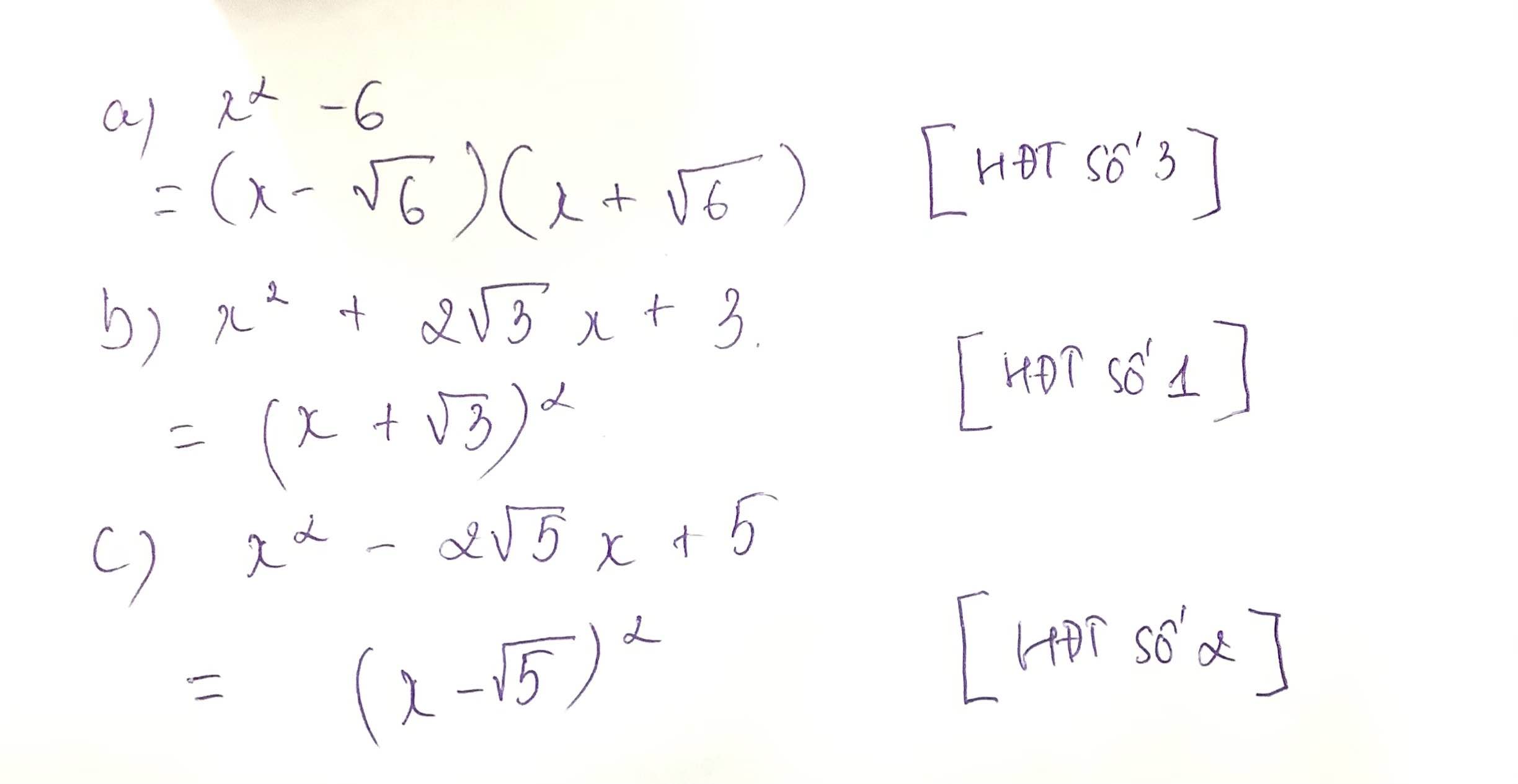
a, \(x.\sqrt{\frac{2}{5}}\) = \(\sqrt{x^2}.\sqrt{\frac{2}{5}}\) = \(\sqrt{\frac{x^2.2}{5}}\)
b, \(\left(x-5\right).\sqrt{\frac{x}{25-x^2}}\)= \(\sqrt{\left(x-5\right)^2}\). \(\sqrt{\frac{x}{\left(5-x\right)\left(5+x\right)}}\) = \(\sqrt{\frac{\left(x-5\right)^2.x}{\left(x-5\right)\left(x+5\right)}}\)= \(\sqrt{\frac{x.\left(x-5\right)}{x+5}}\)
c,\(x.\sqrt{\frac{7}{x^2}}\) = \(\sqrt{x^2}\). \(\sqrt{\frac{7}{x^2}}\) = \(\sqrt{\frac{x^2.7}{x^2}}\) = \(\sqrt{7}\)