Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

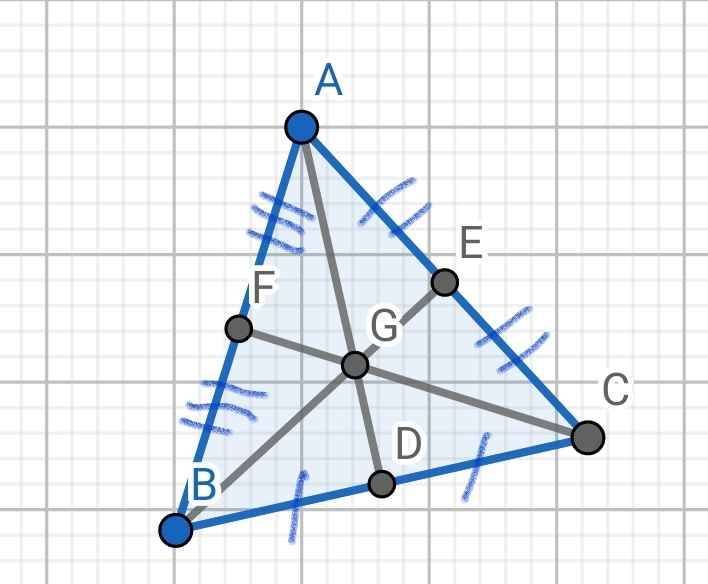
a) Do ∆ABC đều
⇒ AB = AC = BC và ∠A = ∠B = ∠C = 60⁰
Do AD, BE, CF là ba đường trung tuyến
⇒ F, E, D lần lượt là trung điểm của AB, AC, BC
⇒ AF = BF = AE = CE = BD = CD
Xét ∆BEC và ∆CFB có:
CE = BF (cmt)
BC chung
∠BCE = ∠CBF = 60⁰
⇒ ∆BEC = ∆CBF (c-g-c)
⇒ BE = CF (hai cạnh tương ứng) (1)
Xét ∆ADC và ∆CFA có:
AC chung
CD = AF (cmt)
∠ACD = ∠CAF = 60⁰
⇒ ∆ADC = ∆CFA (c-g-c)
⇒ AD = CF (hai cạnh tương ứng) (2)
Từ (1) và (2) ⇒ AD = BE = CF (3)
b) Do AD là đường trung tuyến ứng với đỉnh A
⇒ AG = 2/3 AD (4)
Do BE là đường trung tuyến ứng với đỉnh B
⇒ BG = 2/3 BE (5)
Do CF là đường trung tuyến ứng với đỉnh C
⇒ CG = 2/3 CF (6)
Từ (3), (4), (5), (6) ⇒ AG = BG = CG

a: XétΔABD và ΔACD có
AB=AC
AD chung
BD=CD
Do đó:ΔABD=ΔACD
b: Ta có: ΔABC cân tại A
mà AD là đường trung tuyến
nên AD là đường cao
c: BD=CD=8/2=4(cm)
nên AD=3(cm)