Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

a. \(R=\dfrac{\left(R1+R2\right)R3}{R1+R2+R3}=\dfrac{\left(80+40\right)60}{80+40+60}=40\Omega\)
b. \(U=U12=U3=IR=40.0,15=6V\)(R12//R3)
\(\left\{{}\begin{matrix}I3=U3:R3=6:60=0,1A\\I12=I1=I2=U12:R12=6:\left(80+40\right)=0,05A\left(R1ntR2\right)\end{matrix}\right.\)

Cách 1:
a) Nhận xét: Đoạn mạch gồm hai đoạn mạch con AM (chỉ gồm R1) ghép nối tiếp với MB ( gồm R2 // với R1).
Điện trở tương đương của đoạn mạch là:
Rtđ = RAM + RMB =
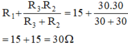
b)
Cường độ dòng điện qua điện trở R1 chính là cường độ dòng điện qua mạch chính:
I1 = I = UAB /Rtđ = 12/30 = 0,4A
Hiệu điện thế giữa hai đầu dây điện trở R1 là: U1 = R1.I1 = 15.0,4 = 6 V.
Hiệu điện thế giữa hai đầu dây điện trở R2 và R3 là:
U2 = U3 = UMB = UAB – UAM = 12 – 6 = 6V
Vì R2 = R3 nên cường độ dòng điện qua R2 và R3 là: I2 = I3 = U3/R3 = 6/30 = 0,2A
Cách 2: Áp dụng cho câu b (có sử dụng kết quả câu a)
Vì R1 ghép nối tiếp với đoạn mạch RAM nên ta có:
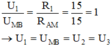
(vì MB chứa R2 //R3 nên UMB = U2 = U3).
Mà U1 + UMB = UAB → U1 = UMB = U2 = U3 = UAB /2 = 12/2 =6 V
→ Cường độ dòng điện qua các điện trở là:
I1 = U1/R1 = 6/15 = 0,4A; I2 = U2/R2 = 6/30 = 0,2A;
I3 = U3/R3 = 6/30 = 0,2A;
(hoặc I3 = I1 –I2 = 0,4 – 0,2 = 0,2 A)

Bạn tự làm tóm tắt nhé!
a. Điện trở tương đương: Rtđ = (R1.R2) : (R1 + R2) = (20.30) : (20 + 30) = 12 (\(\Omega\))
b. Hiệu điện thế của đoạn mạch AB: U = Rtđ.I = 12.1,2 = 14, 4 (V)
Do mạch mắc song song nên U = U1 = U2 = 14,4 (V)
c. Cường độ dòng điện qua R1 và R2:
I1 = U1 : R1 = 14,4 : 20 = 0,72 (A)
I2 = U2 : R2 = 14,4 : 30 = 0, 48 (A)

\(MCD:\left(R2//R3\right)ntR1\)
\(\rightarrow R=\dfrac{R2\cdot R3}{R2+R3}+R1=\dfrac{10\cdot12}{10+12}+10=\dfrac{170}{11}\Omega\)
\(I=I1=I23=U:R=24:\dfrac{170}{11}=\dfrac{132}{85}A\)
\(\rightarrow U1=I1\cdot R1=\dfrac{132}{85}\cdot10=\dfrac{264}{17}V\)
\(\rightarrow U23=U2=U3=U-U1=24-\dfrac{264}{17}=\dfrac{144}{17}V\)
\(\rightarrow\left\{{}\begin{matrix}I2=U2:R2=\dfrac{144}{17}:10=\dfrac{72}{85}A\\I3=U3:R3=\dfrac{144}{17}:12=\dfrac{12}{17}A\end{matrix}\right.\)
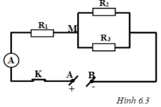

Bữa sau bạn ko gửi dc hình thì hãy ghi trc mạch có dạng j ra nha