Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

\(a,=\frac{7-1}{1.3.7}+\frac{9-3}{3.7.9}+\frac{13-7}{7.9.13}+\frac{15-9}{9.13.15}\)\(+\frac{19-13}{13.15.19}\)
\(=\frac{1}{1.3}-\frac{1}{3.7}+\frac{1}{3.7}-\frac{1}{7.9}+\frac{1}{7.9}-\frac{1}{9.13}+\frac{1}{9.13}-\frac{1}{13.15}+\frac{1}{13.15}-\frac{1}{15.19}\)
\(=\frac{1}{1.3}-\frac{1}{15.19}=\frac{95}{285}-\frac{1}{285}=\frac{94}{285}\)
\(b,=\frac{1}{6}.\left(\frac{6}{1.3.7}+\frac{6}{3.7.9}+\frac{6}{7.9.13}+\frac{6}{9.13.15}+\frac{6}{13.15.19}\right)\)
làm giống như trên
\(c,=\frac{1}{8}.\left(\frac{1}{1.2.3}+\frac{1}{2.3.4}+\frac{1}{3.4.5}+...+\frac{1}{48.49.50}\right)\)
\(=\frac{1}{16}.\left(\frac{2}{1.2.3}+\frac{2}{2.3.4}+\frac{2}{3.4.5}+...+\frac{2}{48.49.50}\right)\)
\(=\frac{1}{16}.\left(\frac{3-1}{1.2.3}+\frac{4-2}{2.3.4}+\frac{5-3}{3.4.5}+...+\frac{50-48}{48.49.50}\right)\)
\(=\frac{1}{16}.\left(\frac{1}{1.2}-\frac{1}{2.3}+\frac{1}{2.3}-\frac{1}{3.4}+\frac{1}{3.4}-\frac{1}{4.5}+...+\frac{1}{48.49}-\frac{1}{49.50}\right)\)
\(=\frac{1}{16}.\left(\frac{1}{2}-\frac{1}{2450}\right)=\frac{1}{16}.\left(\frac{1225}{2450}-\frac{1}{2450}\right)=\frac{153}{4900}\)
\(d,=\frac{5}{7}.\left(\frac{7}{1.5.8}+\frac{7}{5.8.12}+\frac{7}{8.12.15}+...+\frac{7}{33.36.40}\right)\)
\(=\frac{5}{7}.\left(\frac{8-1}{1.5.8}+\frac{12-5}{5.8.12}+\frac{15-8}{8.12.15}+...+\frac{40-33}{33.36.40}\right)\)
\(=\frac{5}{7}.\left(\frac{1}{1.5}-\frac{1}{5.8}+\frac{1}{5.8}-\frac{1}{8.12}+\frac{1}{8.12}-\frac{1}{12.15}+...+\frac{1}{33.36}-\frac{1}{36.40}\right)\)
\(=\frac{5}{7}.\left(\frac{1}{5}-\frac{1}{1440}\right)=\frac{5}{7}.\left(\frac{288}{1440}-\frac{1}{1440}\right)=\frac{41}{288}\)
P/S: . là nhân nha

bạn ơi tại sao bạn lại ra kết quả nh vậyke chi tiết hơn được không vậy

1.3.77−1+3.7.99−3+7.9.1313−7+9.13.1515−9+\frac{19-13}{13.15.19}+13.15.1919−13
=\frac{1}{1.3}-\frac{1}{3.7}+\frac{1}{3.7}-\frac{1}{7.9}+\frac{1}{7.9}-\frac{1}{9.13}+\frac{1}{9.13}-\frac{1}{13.15}+\frac{1}{13.15}-\frac{1}{15.19}=1.31−3.71+3.71−7.91+7.91−9.131+9.131−13.151+13.151−15.191
=\frac{1}{1.3}-\frac{1}{15.19}=\frac{95}{285}-\frac{1}{285}=\frac{94}{285}=1.31−15.191=28595−2851=28594
b,=\frac{1}{6}.\left(\frac{6}{1.3.7}+\frac{6}{3.7.9}+\frac{6}{7.9.13}+\frac{6}{9.13.15}+\frac{6}{13.15.19}\right)b,=61.(1.3.76+3.7.96+7.9.136+9.13.156+13.15.196)
làm giống như trên
c,=\frac{1}{8}.\left(\frac{1}{1.2.3}+\frac{1}{2.3.4}+\frac{1}{3.4.5}+...+\frac{1}{48.49.50}\right)c,=81.(1.2.31+2.3.41+3.4.51+...+48.49.501)
=\frac{1}{16}.\left(\frac{2}{1.2.3}+\frac{2}{2.3.4}+\frac{2}{3.4.5}+...+\frac{2}{48.49.50}\right)=161.(1.2.32+2.3.42+3.4.52+...+48.49.502)
=\frac{1}{16}.\left(\frac{3-1}{1.2.3}+\frac{4-2}{2.3.4}+\frac{5-3}{3.4.5}+...+\frac{50-48}{48.49.50}\right)=161.(1.2.33−1+2.3.44−2+3.4.55−3+...+48.49.5050−48)
=\frac{1}{16}.\left(\frac{1}{1.2}-\frac{1}{2.3}+\frac{1}{2.3}-\frac{1}{3.4}+\frac{1}{3.4}-\frac{1}{4.5}+...+\frac{1}{48.49}-\frac{1}{49.50}\right)=161.(1.21−2.31+2.31−3.41+3.41−4.51+...+48.491−49.501)
=\frac{1}{16}.\left(\frac{1}{2}-\frac{1}{2450}\right)=\frac{1}{16}.\left(\frac{1225}{2450}-\frac{1}{2450}\right)=\frac{153}{4900}=161.(21−24501)=161.(24501225−24501)=4900153
d,=\frac{5}{7}.\left(\frac{7}{1.5.8}+\frac{7}{5.8.12}+\frac{7}{8.12.15}+...+\frac{7}{33.36.40}\right)d,=75.(1.5.87+5.8.127+8.12.157+...+33.36.407)
=\frac{5}{7}.\left(\frac{8-1}{1.5.8}+\frac{12-5}{5.8.12}+\frac{15-8}{8.12.15}+...+\frac{40-33}{33.36.40}\right)=75.(1.5.88−1+5.8.1212−5+8.12.1515−8+...+33.36.4040−33)
=\frac{5}{7}.\left(\frac{1}{1.5}-\frac{1}{5.8}+\frac{1}{5.8}-\frac{1}{8.12}+\frac{1}{8.12}-\frac{1}{12.15}+...+\frac{1}{33.36}-\frac{1}{36.40}\right)=75.(1.51−5.81+5.81−8.121+8.121−12.151+...+33.361−36.401)
=\frac{5}{7}.\left(\frac{1}{5}-\frac{1}{1440}\right)=\frac{5}{7}.\left(\frac{288}{1440}-\frac{1}{1440}\right)=\frac{41}{288}=75.(51−14401)=75.(1440288−14401)=28841
P/S: . là nhân nha

a) \(\frac{1.3+3.5+5.7+7.9}{3.6+9.10+15.14+21.18}\)
= \(\frac{1.3+3.5+5.7+7.9}{1.3.2.3+3.5.2.3+5.7.2.3+7.9.2.3}\)
= \(\frac{1.3+3.5+5.7+7.9}{1.3.6+3.5.6+5.7.6+7.9.6}\)
= \(\frac{1.3+3.5+5.7+7.9}{6.\left(1.3+3.5+5.7+7.9\right)}=\frac{1}{6}\)
Dấu "." là dấu nhân cấp 2
b) \(\frac{1.2+2.3+3.4+4.5}{3.6+6.9+9.12+12.15}\)
= \(\frac{1.2+2.3+3.4+4.5}{1.2.3.3+2.3.3.3+3.4.3.3+4.5.3.3}\)
= \(\frac{1.2+2.3+3.4+4.5}{1.2.9+2.3.9+3.4.9+4.5.9}\)
= \(\frac{1.2+2.3+3.4+4.5}{9.\left(1.2+2.3+3.4+4.5\right)}=\frac{1}{9}\)
Dấu "." là dấu nhân cấp 2
c) \(\frac{0,3+\frac{3}{7}+\frac{3}{11}}{0,4+\frac{4}{7}+\frac{4}{11}}\)= \(\frac{\frac{3}{10}+\frac{3}{7}+\frac{3}{11}}{\frac{4}{10}+\frac{4}{7}+\frac{4}{11}}\)= \(\frac{3.\left(\frac{1}{10}+\frac{1}{7}+\frac{1}{11}\right)}{4.\left(\frac{1}{10}+\frac{1}{7}+\frac{1}{11}\right)}=\frac{3}{4}\)

a) Cách 1 : Cách 2
1 + 3 +5 + 7 + 9 + 11 + 13 + 15 + 17 + 19 1 + 3 +5 + 7 + 9 + 11 + 13 + 15 + 17 + 19
=(1 + 19) + (3 + 17) +.... + (9 + 11) Áp dụng công thức tính dãy số ta có :
= 20 + 20 + ... + 20 \(\frac{\left[\left(19-1\right):2+1\right].\left(19+1\right)}{2}=\frac{10.20}{2}=10.10=100\)
= 20 x 5 = 100
b) giống bài a nhưng cách 1 làm dài lắm , mình sẽ làm cách 2
áp dụng công thức tính dãy số ta có:
\(\frac{\left[\left(200-4\right):4+1\right].\left(200+4\right)}{2}=\frac{50.204}{2}=50.102=5100\)

a.1+3+5+7+9+11+13+15+17+19
muốn tính tổng của dãy ta lấy tổng số đầu và cuối nhân số các số hạng rồi chia 2.
tổng của dãy:(19+1)x10:2=100

Bài giải
\(\frac{2}{3}+\frac{3}{4}+\frac{4}{5}=\frac{40}{60}+\frac{45}{60}+\frac{48}{60}=\frac{133}{60}\)
\(\frac{8}{5}+\frac{7}{6}+\frac{10}{9}+\frac{1}{2}=\frac{144}{90}+\frac{105}{90}+\frac{100}{90}+\frac{45}{90}=\frac{394}{90}\)
\(\frac{15}{17}-\frac{11}{13}+\frac{3}{26}=\frac{390}{442}+\frac{374}{442}+\frac{51}{442}=\frac{815}{442}\)
\(\frac{9}{12}\text{ x }\frac{4}{3}\text{ : }\frac{8}{5}=\frac{9}{12}\text{ x }\frac{4}{3}\text{ x }\frac{5}{8}=\frac{9\text{ x }4\text{ x }5}{12\text{ x }3\text{ x }8}=\frac{5}{8}\)
\(\frac{4}{5}\text{ x }\frac{15}{8}\text{ : }\frac{5}{7}=\frac{4}{5}\text{ x }\frac{15}{8}\text{ x }\frac{7}{5}=\frac{4\text{ x }15\text{ x }7}{5\text{ x }8\text{ x }5}=\frac{21}{10}\)
\(\frac{2}{3}+\frac{3}{4}+\frac{4}{5}=\frac{40}{60}+\frac{45}{60}+\frac{48}{60}=\frac{133}{60}\)
\(\frac{8}{5}+\frac{7}{6}+\frac{10}{9}+\frac{1}{2}=\frac{144}{90}+\frac{105}{90}+\frac{100}{90}+\frac{45}{90}=\frac{197}{45}\)
\(\frac{15}{17}-\frac{11}{13}+\frac{1}{26}=\frac{390}{442}+\frac{374}{442}+\frac{51}{442}=\frac{815}{442}\)
\(\frac{9}{12}\times\frac{4}{3}:\frac{8}{5}=1:\frac{8}{5}=\frac{5}{8}\)
\(\frac{4}{5}\times\frac{15}{8}:\frac{5}{7}=\frac{3}{2}:\frac{5}{7}=\frac{21}{10}\)

Bài 2. > , < , = ?
5/7 < 4/3 2/5 < 6/10 1/4 = 3/12 27/36 >
2/9 7/6 > 7/9
7/2 = 2/7 15/23 < 1 27/9 > 2 14/15 < 1 51/17 < 4
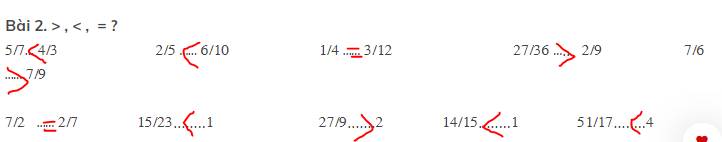
Bài 1:
\(A=\frac{5}{3.6}+\frac{5}{6.9}+....+\frac{5}{96.99}\)
\(\Rightarrow\frac{3}{5}A=\frac{3}{3.6}+\frac{3}{6.9}+....+\frac{3}{96.99}\)
\(\Rightarrow\frac{3}{5}A=\frac{1}{3}-\frac{1}{6}+\frac{1}{6}-\frac{1}{9}+...+\frac{1}{96}-\frac{1}{99}\)
\(=\frac{1}{3}-\frac{1}{99}=\frac{32}{99}\)
\(\Rightarrow A=\frac{32}{99}\div\frac{3}{5}=\frac{160}{297}\)
Bái 2:
\(B=\frac{2}{3.7}+\frac{2}{7.11}+...+\frac{2}{99.103}\)
\(\Rightarrow2B=\frac{4}{3.7}+\frac{4}{7.11}+....+\frac{4}{99.103}\)
\(\Rightarrow2B=\frac{1}{3}-\frac{1}{7}+\frac{1}{7}-\frac{1}{11}+....+\frac{1}{99}-\frac{1}{103}\)
\(=\frac{1}{3}-\frac{1}{103}=\frac{100}{309}\)
\(\Rightarrow B=\frac{100}{309}\div2=\frac{50}{309}\)
Bài 1:
Ta có:
\(\frac{5}{n.\left(n+3\right)}=\frac{5}{3}.\frac{3}{n.\left(n+3\right)}=\frac{5}{3}.\frac{\left(n+3\right)-n}{n.\left(n+3\right)}=\frac{5}{3}.\left[\frac{n+3}{n.\left(n+3\right)}-\frac{n}{n\left(n+3\right)}\right]\)\(=\frac{5}{3}\left(\frac{1}{n}-\frac{1}{n+3}\right)\)
\(\frac{5}{3.6}+\frac{5}{6.9}+\frac{5}{9.12}+...+\frac{5}{96.99}=\frac{5}{3}\left(\frac{1}{3}-\frac{1}{6}+\frac{1}{6}-\frac{1}{9}+...+\frac{1}{96}-\frac{1}{99}\right)\)