Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

a.
$12x^3y-24x^2y^2+12xy^3=12xy(x^2-2xy+y^2)=12xy(x-y)^2$
b.
$x^2-6x+xy-6y=(x^2+xy)-(6x+6y)=x(x+y)-6(x+y)=(x-6)(x+y)$
c.
$2x^2+2xy-x-y=2x(x+y)-(x+y)=(x+y)(2x-1)$
d.
$x^3-3x^2+3x-1=(x-1)^3$
e.
$3x^2-3y^2-12x-12y=(3x^2-3y^2)-(12x+12y)$
$=3(x-y)(x+y)-12(x+y)=(x+y)[3(x-y)-12]=3(x-y)(x-y-4)$
f.
$x^2-2xy-x^2+4y^2=4y^2-2xy=2y(2y-x)$

\(a,=4x^2+3xy-y^2+4xy-4x^2=7xy-y^2\\ b,=x^2-9-x^3+3x+x^2-3=-x^3+2x^2+3x-12\\ c,=-2x^2+12x-18+5x^2+4x-1=3x^2+16x-19\\ d,=8x^3+1-3x^3+6x^2=5x^3+6x^2+1\\ e,=\left(3x^2+4x+15x+20\right):\left(3x+4\right)\\ =\left(3x+4\right)\left(x+5\right):\left(3x+4\right)\\ =x+5\\ f,=\left(x^3+4x^2-3x+3x^2+12x-9+3x+3\right):\left(x^2+4x-3\right)\\ =\left[\left(x^2+4x-3\right)\left(x+3\right)+3x+3\right]:\left(x^2+4x-3\right)\\ =x+3\left(dư.3x+3\right)\)

\(a,=6x^2+23x+21-\left(6x^2+23x-55\right)\\ =76\left(đpcm\right)\\ b,=3x^4+6x^3+9x^2-2x^3-4x^2-6x+x^2+2x+3-4x^3+4x-3x^4-6x^2\\ =3\left(đpcm\right)\)

a.
$x^2-y^2-2x+2y=(x^2-y^2)-(2x-2y)=(x-y)(x+y)-2(x-y)=(x-y)(x+y-2)$
b.
$x^2(x-1)+16(1-x)=x^2(x-1)-16(x-1)=(x-1)(x^2-16)=(x-1)(x-4)(x+4)$
c.
$x^2+4x-y^2+4=(x^2+4x+4)-y^2=(x+2)^2-y^2=(x+2-y)(x+2+y)$
d.
$x^3-3x^2-3x+1=(x^3+1)-(3x^2+3x)=(x+1)(x^2-x+1)-3x(x+1)$
$=(x+1)(x^2-4x+1)$
e.
$x^4+4y^4=(x^2)^2+(2y^2)^2+2.x^2.2y^2-4x^2y^2$
$=(x^2+2y^2)^2-(2xy)^2=(x^2+2y^2-2xy)(x^2+2y^2+2xy)$
f.
$x^4-13x^2+36=(x^4-4x^2)-(9x^2-36)$
$=x^2(x^2-4)-9(x^2-4)=(x^2-9)(x^2-4)=(x-3)(x+3)(x-2)(x+2)$
g.
$(x^2+x)^2+4x^2+4x-12=(x^2+x)^2+4(x^2+x)-12$
$=(x^2+x)^2-2(x^2+x)+6(x^2+x)-12$
$=(x^2+x)(x^2+x-2)+6(x^2+x-2)=(x^2+x-2)(x^2+x+6)$
$=[x(x-1)+2(x-1)](x^2+x+6)=(x-1)(x+2)(x^2+x+6)$
h.
$x^6+2x^5+x^4-2x^3-2x^2+1$
$=(x^6+2x^5+x^4)-(2x^3+2x^2)+1$
$=(x^3+x^2)^2-2(x^3+x^2)+1=(x^3+x^2-1)^2$

\(1,\\ a,=3x^3-2x^2+5x\\ b,=2x^3y^2+\dfrac{2}{9}x^4y^2-\dfrac{1}{3}x^2y^3\\ c,=x^2-2x+6x-12=x^2+4x-12\\ 2,\\ a,\Rightarrow6x-9+4-2x=-3\\ \Rightarrow4x=2\Rightarrow x=\dfrac{1}{2}\\ b,\Rightarrow5x-2x^2+2x^2-2x=13\\ \Rightarrow3x=13\Rightarrow x=\dfrac{13}{3}\\ c,\Rightarrow5x^2-5x-5x^2+7x-10x+14=6\\ \Rightarrow-8x=-8\Rightarrow x=1\\ d,\Rightarrow6x^2+9x-6x^2+4x-15x+10=8\\ \Rightarrow-2x=-2\Rightarrow x=1\)
\(3,\\ A=2x^2+x-x^3-2x^2+x^3-x+3=3\\ B=6x^2-10x+33x-55-6x^2-14x-9x-21=-76\)

a: Ta có: \(x^2-4y^2-2x-4y\)
\(=\left(x-2y\right)\left(x+2y\right)-2\left(x+2y\right)\)
\(=\left(x+2y\right)\left(x-2y-2\right)\)
c: Ta có: \(x^3+2x^2y-x-2y\)
\(=x^2\left(x+2y\right)-\left(x+2y\right)\)
\(=\left(x+2y\right)\left(x-1\right)\left(x+1\right)\)
d: Ta có: \(3x^2-3y^2-2\cdot\left(x-y\right)^2\)
\(=3\left(x-y\right)\left(x+y\right)-2\cdot\left(x-y\right)^2\)
\(=\left(x-y\right)\left(3x+3y-2x+2y\right)\)
\(=\left(x-y\right)\left(x+5y\right)\)
e: Ta có: \(x^3-4x^2-9x+36\)
\(=x^2\left(x-4\right)-9\left(x-4\right)\)
\(=\left(x-4\right)\left(x-3\right)\left(x+3\right)\)
f: Ta có: \(x^2-y^2-2x-2y\)
\(=\left(x-y\right)\left(x+y\right)-2\left(x+y\right)\)
\(=\left(x+y\right)\left(x-y-2\right)\)

a) (x – 1)(x2 + x + 1) – 2x = x(x – 1)(x + 1)
⇔ x3 – 1 – 2x = x(x2 – 1)
⇔ x2 – 1 – 2x = x3 – x
⇔ -2x + x = 1 ⇔ - x = 1 ⇔ x = -1
Tập nghiệm của phương trình: S = { -1}
b) x2 – 3x – 4 = 0
⇔ x2 – 4x + x – 4 = 0 ⇔ x(x – 4) + (x – 4) = 0
⇔ (x – 4)(x + 1) = 0 ⇔ x – 4 = 0 hoặc x + 1 = 0
⇔ x = 4 hoặc x = -1
Tập nghiệm của phương trình: S = {4; -1}
c) ĐKXĐ : x – 1 ≠ 0 và x2 + x + 1 ≠ 0 (khi đó : x3 – 1 = (x – 1)(x2 + x + 1) ≠ 0)
⇔ x ≠ 1
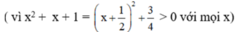
Quy đồng mẫu thức hai vế:
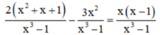
Khử mẫu, ta được: 2x2 + 2x + 2 – 3x2 = x2 – x
⇔ -2x2 + 3x + 2 = 0 ⇔ 2x2 – 3x – 2 = 0
⇔ 2x2 – 4x + x – 2 = 0 ⇔ 2x(x – 2) + (x – 2) = 0
⇔ (x – 2)(2x + 1) = 0 ⇔ x – 2 = 0 hoặc 2x + 1 = 0
⇔ x = 2 hoặc x = -1/2(thỏa mãn ĐKXĐ)
Tập nghiệm của phương trình : S = {2 ; -1/2}
d) ĐKXĐ : x – 5 ≠ 0 và x – 1 ≠ 0 (khi đó : x2 – 6x + 5 = (x – 5)(x – 1) ≠ 0)
Quy đồng mẫu thức hai vế :
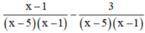
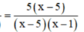
Khử mẫu, ta được : x – 1 – 3 = 5x – 25 ⇔ -4x = -21
⇔ x = 21/4 (thỏa mãn ĐKXĐ)
Tập nghiệm của phương trình : S = {21/4}

kho the