Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

Chọn C
+ Để trong quá trình dao động ba vật luôn thẳng hàng thì: ![]()
=> 2x2 = x1 +x3 => x1 = 2x2 – x3
+ Ta có thể sử dụng phương pháp tổng hợp dao động bằng số phức trên máy tính => x1 = 20cos(20t + π/2) cm.

Đáp án A
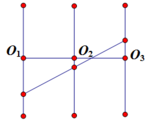
Vì 3 vật luôn thẳng hàng nên dễ dàng nhận ra li độ của x2 sẽ luôn là trung bình cộng của x1 và x3. = > 2 x 2 = x 1 + x 3 .
Bấm máy tính để tổng hợp dao động, dễ dàng tìm được x 3 = 3 2 cos 20 π t − 0 , 25 π (cm)

Chọn đáp án A
Vì 3 vật luôn nằm trên một đường thẳng nên ta có:

Bấm máy tính theo số phức như dạng tổng hợp dao động điều hòa ta tính ra được:
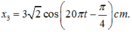

Đáp án A
Vì 3 vật luôn nằm trên một đường thẳng nên ta có : x 2 = x 1 + x 3 2 ⇒ x 3 = 2 x 2 - x 1
Bấm máy tính theo số phức như dạng tổng hợp dao động điều hòa ta tính ra được :
x 3 = 3 2 cos ( 20 πt - 0 , 25 π ) cm

Chọn C
+ ω = 2π : T = 20 rad/s.
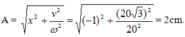
+ t = 0: x = 2cosφ = -1 => 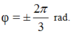
v = -40 sinφ > 0 => sinφ < 0 => ![]()
Vậy: x = 2 cos(20t - 2π/3) = 2 sin(20t - π/6) cm.

Đáp án C
Để 3 vật luôn nằm trên một đường thẳng thì: x 2 = x 1 + x 3 2 ⇒ x 3 = 2 x 2 - x 1
Chuyển máy về dạng tính số phức và bấm nhanh:
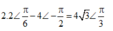
Vậy phương trình dao động của vật 3: x = 4 3 cos ( 5 πt + π 3 ) ( c m )

Chọn A
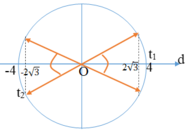
Khoảng cách giữa hai vật theo phương Ox là:
![]()
Theo bài ra ta có d ≥ 2√3
Trong khoảng t1 = 1/24 s đến t2 = 1/3s = t1 + T/2 +T/12, d có độ lớn không nhỏ hơn 2√3 trong khoảng thời gian là:
∆t = T/12 + 2. T/12 = 1/8s.

Đáp án B
Phương pháp: Sử dụng định lý Py-ta-go và lí thuyết về dao động điều hòa
Cách giải :
Khoảng cách giữa hai chất điểm A và B được xác định theo công thức: d = x 2 + y 2
Theo đề bài ta có:
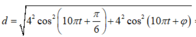
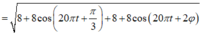
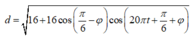
=> Để khoảng cách giữa AB không thay đổi thì khoảng cách này phải không phụ thuộc vào t
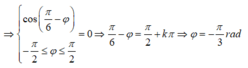
Đáp án A