Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

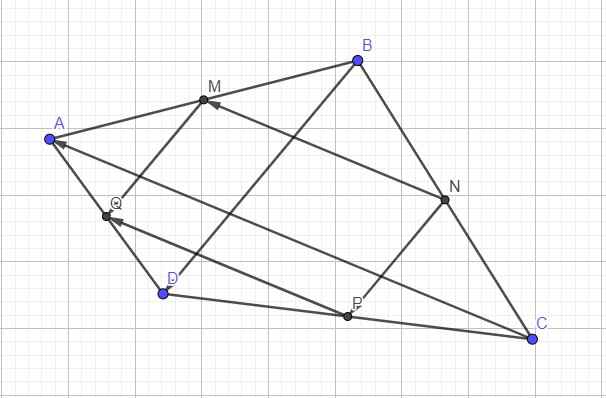
1) Các vecto bằng vecto EF là:
\(\overrightarrow{EF}=\overrightarrow{DO}=\overrightarrow{OA}=\overrightarrow{CB}\)

Do M là trung điểm AB, Q là trung điểm AD
\(\Rightarrow\) MQ là đường trung bình tam giác ABD
\(\Rightarrow\overrightarrow{MQ}=\dfrac{1}{2}\overrightarrow{BD}\)
Tương tự ta có NP là đường trung bình tam giác BCD
\(\Rightarrow\overrightarrow{NP}=\dfrac{1}{2}\overrightarrow{BD}\)
\(\Rightarrow\overrightarrow{NP}=\overrightarrow{MQ}\)
b. MN là đường trung bình tam giác ABC
\(\Rightarrow\overrightarrow{NM}=\dfrac{1}{2}\overrightarrow{CA}\)
PQ là đường trung bình tam giác ACD
\(\Rightarrow\overrightarrow{PQ}=\dfrac{1}{2}\overrightarrow{CA}\)
\(\Rightarrow\overrightarrow{PQ}=\overrightarrow{NM}\)
Bài 1 :
- Lấy điểm D đối xứng với A qua BC .
Mà tam giác ABC đều .
=> Tứ giác ABCD là hình thoi
=> Tứ giác ABCD là hình bình hành .
=> \(\overrightarrow{AC}=\overrightarrow{BD}\)
Ta có : \(\overrightarrow{AB}+\overrightarrow{AC}=\overrightarrow{AB}+\overrightarrow{BD}=\overrightarrow{AD}\)
Ta có : Tứ giác ABCD là hình bình hành ( cmt )
=> \(\overrightarrow{CA}=\overrightarrow{DB}\)
=> \(\overrightarrow{CA}+\overrightarrow{BA}=\overrightarrow{DB}+\overrightarrow{BA}=\overrightarrow{DA}\)
Ta có : \(AD=\left|\overrightarrow{AD}\right|=\left|\overrightarrow{DA}\right|=2AM\) ( Tứ giác ABCD là hình thoi )
Ta có : M là trung điểm BC .
=> \(BM=\frac{1}{2}BC=\frac{a}{2}\)
- Áp dụng định lý pi - ta - go vào tam giác AMB vuông tại M .
=> \(AM^2+\frac{a^2}{4}=a^2\)
=> \(2AM=2\sqrt{a^2-\frac{a^2}{4}}=2\sqrt{\frac{3a^2}{4}}=2\left(\frac{a\sqrt{3}}{2}\right)=a\sqrt{3}\)
b, Ta có : M, N là trung điểm của BC và AC .
=> \(\left\{{}\begin{matrix}2\overrightarrow{AM}=\overrightarrow{AB}+\overrightarrow{AC}\\2\overrightarrow{BN}=\overrightarrow{BA}+\overrightarrow{BC}\end{matrix}\right.\)
=> \(\overrightarrow{AM}+\overrightarrow{BN}=\frac{1}{2}\left(\overrightarrow{AB}+\overrightarrow{AC}+\overrightarrow{BA}+\overrightarrow{BC}\right)=\frac{1}{2}\left(\overrightarrow{AC}+\overrightarrow{BC}\right)\)
- Lấy E đối xứng với B qua DC .
CMTT : Ta được : \(\overrightarrow{AM}+\overrightarrow{BN}=\frac{1}{2}\left(\overrightarrow{BD}+\overrightarrow{BC}\right)=\frac{1}{2}\overrightarrow{BE}\)
Mà \(\left|\overrightarrow{BE}\right|=\left|\overrightarrow{AD}\right|\)
=> \(\left|\overrightarrow{AM}\right|+\left|\overrightarrow{BN}\right|=\frac{a\sqrt{3}}{2}\)
Bài 2 :
ĐT <=> \(\overrightarrow{CD}-\overrightarrow{CA}+\overrightarrow{EA}-\overrightarrow{ED}=\overrightarrow{0}\)
<=> \(\overrightarrow{AD}+\overrightarrow{DA}=\overrightarrow{0}\) ( đpcm )