Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

\(0,2x+\frac{1}{5}=0\)
\(\Rightarrow0,2x=-\frac{1}{5}\)\(\Rightarrow x=-1\)
Ta có nghiệm là -2 => x = -2
\(a\left(-2\right)-1,5=0\)
Gải ra tìm a => a là hệ số

Nghiệm của đa thức M(x) là \(\dfrac{1}{2}\)
\(\Rightarrow x=\dfrac{1}{2}\) để đa thức M(x) = 0
Thay \(x=\dfrac{1}{2}\), ta có:
\(a.\left(\dfrac{1}{2}\right)^2+5.\dfrac{1}{2}-3=0\\ \Rightarrow\dfrac{1}{4}a+\dfrac{5}{2}=3\\ \Rightarrow\dfrac{1}{4}a=3-\dfrac{5}{2}\\ \Rightarrow\dfrac{1}{4}a=\dfrac{1}{2}\\ \Rightarrow a=\dfrac{1}{2}:\dfrac{1}{4}=2\)
Vậy a = 2. Đa thức M(x) được viết đầy đủ dưới dạng:
\(M\left(x\right)=2x^2+5x-3\)
M(x) có nghiệm là 1/2 nên khi x = 1/2 thì M(x) = 0
\(a\left(\dfrac{1}{2}\right)^2+5.\dfrac{1}{2}-3=0\)
\(\Rightarrow a=2\)
Vậy...

Giải
1) M(x) = -2x+3 ->-2x+3 =0
->x= 3/2
Vậy nghiệm của M(x) là 3/2
2) P(x) =ax+1 có nghiệm là -2
-> P(-2) =a*(-2)+1=0
-> a= 1/2
Vậy hệ số của P(x) là 1/2

a) Ta có f(7) = a7 + b và f(2) + f(3) = (a2+ b) + (a3 + b) = 5a + 2b. Vậy để f(7) = f(2) + f(3), ta cần giải phương trình:
a7 + b = 5a + 2b
Simplifying, ta được: 2a = b.
Vậy điều kiện của a và b để f(7) = f(2) + f(3) là b = 2a.
b) Để tìm nghiệm của P(x), ta cần giải phương trình (x-2)(2x+5) = 0:
(x-2)(2x+5)= 0
→ X-2 = 0 hoặc 2x+5 = 0
→ x = 2 hoặc x = -5/2
Vậy nghiệm của P(x) là x = 2 hoặc x =-5/2.
c) Ta biết rằng đa thức P(x) có 1 nghiệm là -2, vậy ta có thể viết P(x)
dưới dạng:
P(x) = (x+2)(x^3 - 2x^2 + ax - 2)
Từ đó suy ra:
P(-2) = (-2+2)(8 - 4a - 2) = 0
⇔-8a= 16
⇔a = -2
Vậy hệ số a của P(x) là -2.

ta có : \(P\left(\dfrac{-3}{2}\right)=0\)
\(\Leftrightarrow\left(-\dfrac{3}{2}\right)^3-a.\left(-\dfrac{3}{2}\right)^2-2\cdot\dfrac{-3}{2}+4=0\)
\(\Leftrightarrow-\dfrac{27}{8}-\dfrac{9}{4}a+3+4=0\)
\(\Leftrightarrow\cdot\dfrac{9}{4}a=-\dfrac{27}{8}-3-4=-16\)
\(=>a=-16:\dfrac{9}{4}=-\dfrac{64}{9}\)

a) Ta có a.1/3 - 1/2 = 0
=> a.1/3 = 1/2
=> a = 3/2
Vậy a = 3/2
b) Ta có : f(1) = a.1 + b = a + b = -3
=> a + b = -3 (1)
Lại có f(2) = a.2 + b = 2 x a + b = 7
=> 2 x a + b = 7 (2)
Khi đó 2 x a + b - (a + b) = 7 - (-3)
=> 2 x a - a = 10
=> a = 10
=> b = -13
Vậy a = 10 ; b = -13
a ) Ta có : \(a\cdot\frac{1}{3}-\frac{1}{2}=0\)
\(\Rightarrow a\cdot\frac{1}{3}=\frac{1}{2}\)
\(\Rightarrow a=\frac{3}{2}\)
Vậy \(a=\frac{3}{2}\)
b ) Ta có : \(f\left(1\right)=a\cdot1+b=a+b=-3\)
\(\Rightarrow a+b=-3\)(1)
Lại có : \(f\left(2\right)=a\cdot2+b=2\cdot a+b=7\)
\(\Rightarrow2\cdot a+b=7\)(2)
Khi đó : \(2\cdot a+b-\left(a+b\right)=7-\left(3\right)\)
\(\Rightarrow2\cdot a-a=10\)
\(\Rightarrow a=10;b=-13\)
Vậy ...

a/ \(M\left(x\right)=-x^2+5\)
Có \(-x^2\le0\forall x\)
=> \(M\left(x\right)\le5\forall x\)
=> M(x) không có nghiệm.
2/
Thay \(x=\dfrac{1}{2}\) vào đa thức M(x) có
\(M\left(\dfrac{1}{2}\right)=\dfrac{1}{4}a+\dfrac{5}{2}-3=0\)
\(\Leftrightarrow\dfrac{1}{4}a=\dfrac{1}{2}\)
\(\Leftrightarrow a=2\)
Vậy...
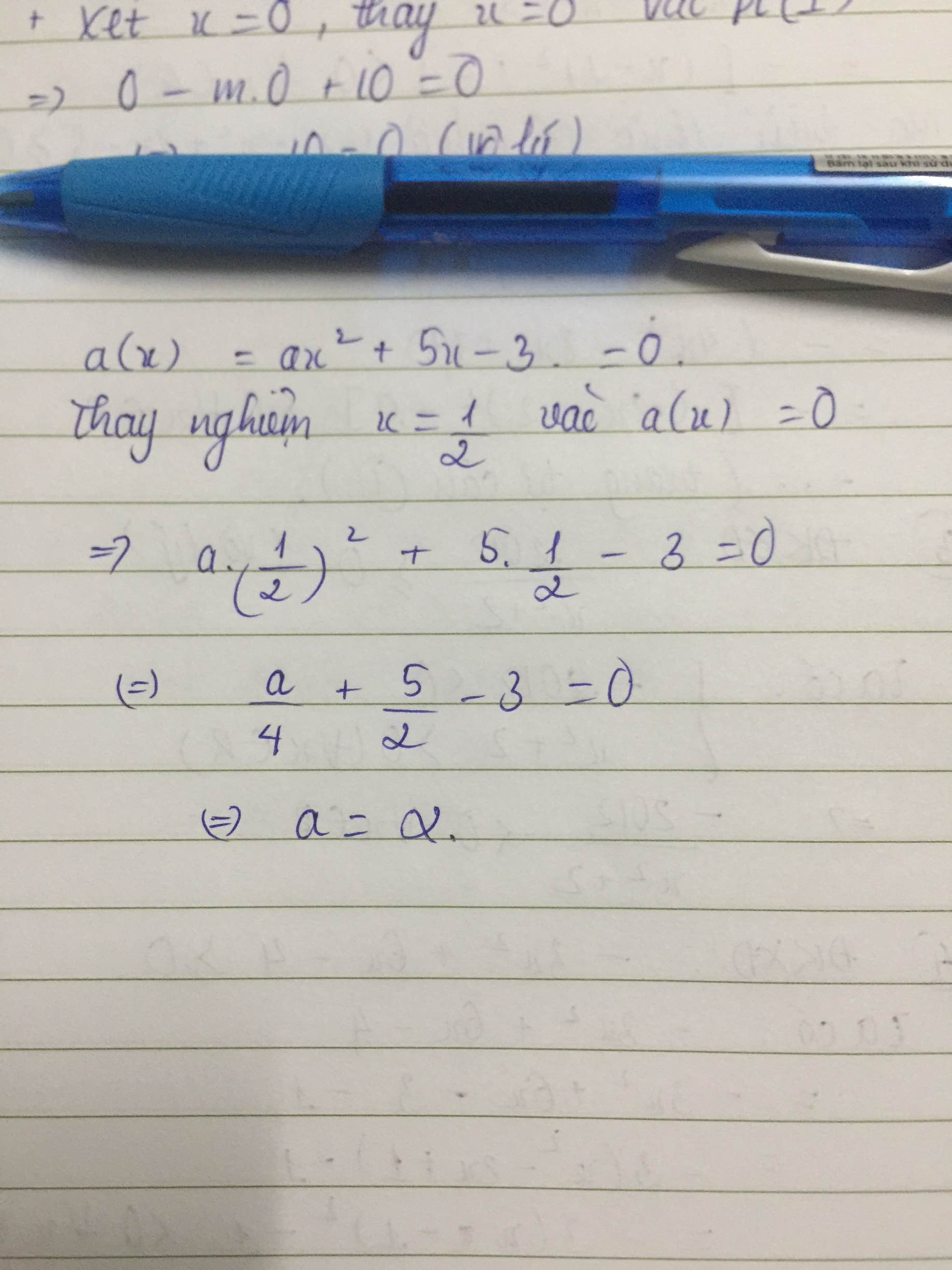
a, Đa thức \(0,2x+\dfrac{1}{5}\) có nghiệm khi \(0,2x+\dfrac{1}{5}=0\)
\(\Rightarrow0,2x=\dfrac{-1}{5}\Rightarrow x=-1\)
Vậy, ...