
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.


\(P=\frac{\sqrt{x}}{\sqrt{x}-1}+\frac{\sqrt{x}-2}{\sqrt{x}-1}\)
ĐKXĐ : \(\hept{\begin{cases}x\ge0\\x\ne1\end{cases}}\)
\(=\frac{\sqrt{x}+\sqrt{x}-2}{\sqrt{x}-1}\)
\(=\frac{2\sqrt{x}-2}{\sqrt{x}-1}\)
\(=\frac{2\left(\sqrt{x}-1\right)}{\sqrt{x}-1}=2\)
=> Với mọi \(\hept{\begin{cases}x\ge0\\x\ne1\end{cases}}\)thì P = 2
Đề sai à --

a: ĐKXĐ: \(\left\{{}\begin{matrix}x\ge0\\x\ne4\end{matrix}\right.\)
Ta có: \(P=\dfrac{\sqrt{x}}{\sqrt{x}+2}+\dfrac{2}{\sqrt{x}-2}-\dfrac{4\sqrt{x}}{x-4}\)
\(=\dfrac{x-2\sqrt{x}+2\sqrt{x}+4-4\sqrt{x}}{\left(\sqrt{x}-2\right)\left(\sqrt{x}+2\right)}\)
\(=\dfrac{\sqrt{x}-2}{\sqrt{x}+2}\)

ta có x+y=\(\sqrt{10}\)=>(x+y)^2=10
A=(x^4+1)(y^4+1)
=x^4.y^4+1+x^4+y^4+2x^2.y^2-2x^2.y^2
=x^4.y^4+1+(x^2+y^2)^2-2x^y^2=x^4.y^4+1+[(x+y)^2-2xy]
=x^4.y^4+1+(10-2xy)-2x^2.y^2
=x^4.y^4+1+100-40xy+4.x^2.y^2-2x^2.y^2
=x^4.y^4+101-40xy+2.x^2.y^2
=(x^4.y^4-8.x^2.y^2+16)+(10.x^2.y^2-40xy+40)+45
=(x^2.y^2-4)^2+10.(xy-2)^2+45\(\ge\)0
dấu = xảy ra \(\Leftrightarrow\)\(\left\{{}\begin{matrix}x+y=\sqrt{10}\\x.y=2\end{matrix}\right.\)
vậy Min A=45
\(\left\{{}\begin{matrix}x+y=\sqrt{10}\\x.y=2\end{matrix}\right.\)là nghiệm pt x^2-\(\sqrt{10}\)x+2
=>\(\Delta\)=(-\(\sqrt{10}\))^2-4.2=2>0
=>\(\left\{{}\begin{matrix}x=\dfrac{\sqrt{10}-\sqrt{2}}{2}\\y=\dfrac{\sqrt{10}+\sqrt{2}}{2}\end{matrix}\right.\)hoặc \(\left\{{}\begin{matrix}x=\dfrac{\sqrt{10}-\sqrt{2}}{2}\\y=\dfrac{\sqrt{10}+\sqrt{2}}{2}\end{matrix}\right.\)

\(A=\dfrac{\left(\sqrt{x}-2\right)^2+1}{\sqrt{x}-2}=\sqrt{x}-2+\dfrac{1}{\sqrt{x}-2}\\ \ge2\sqrt{\left(\sqrt{x}-2\right)\left(\dfrac{1}{\sqrt{x}-2}\right)}=2\cdot1=2\left(BĐT.cauchy\right)\)
Dấu \("="\Leftrightarrow\left(\sqrt{x}-2\right)^2=1\Leftrightarrow\sqrt{x}=3\Leftrightarrow x=9\)
\(A=\dfrac{x-4\sqrt{x}+5}{\sqrt{x}-2}=\dfrac{\left(\sqrt{x}-2\right)^2+1}{\sqrt{x}-2}=\sqrt{x}-2+\dfrac{1}{\sqrt{x}-2}\)
Áp dụng bất đẳng thức Cauchy cho 2 số dương:
\(A=\sqrt{x}-2+\dfrac{1}{\sqrt{x}-2}\ge2\sqrt{\dfrac{\sqrt{x}-2}{\sqrt{x}-2}}=2\)
\(minA=2\Leftrightarrow\sqrt{x}-2=1\Leftrightarrow\sqrt{x}=3\Leftrightarrow x=9\)

\(A=\sqrt{x}+\dfrac{2}{\sqrt{x}}\ge2\cdot\sqrt{\sqrt{x}\cdot\dfrac{2}{\sqrt{x}}}=2\sqrt{2}\)
Dấu '=' xảy ra khi \(\sqrt{x}\cdot\sqrt{x}=2\)
hay \(x=2\)
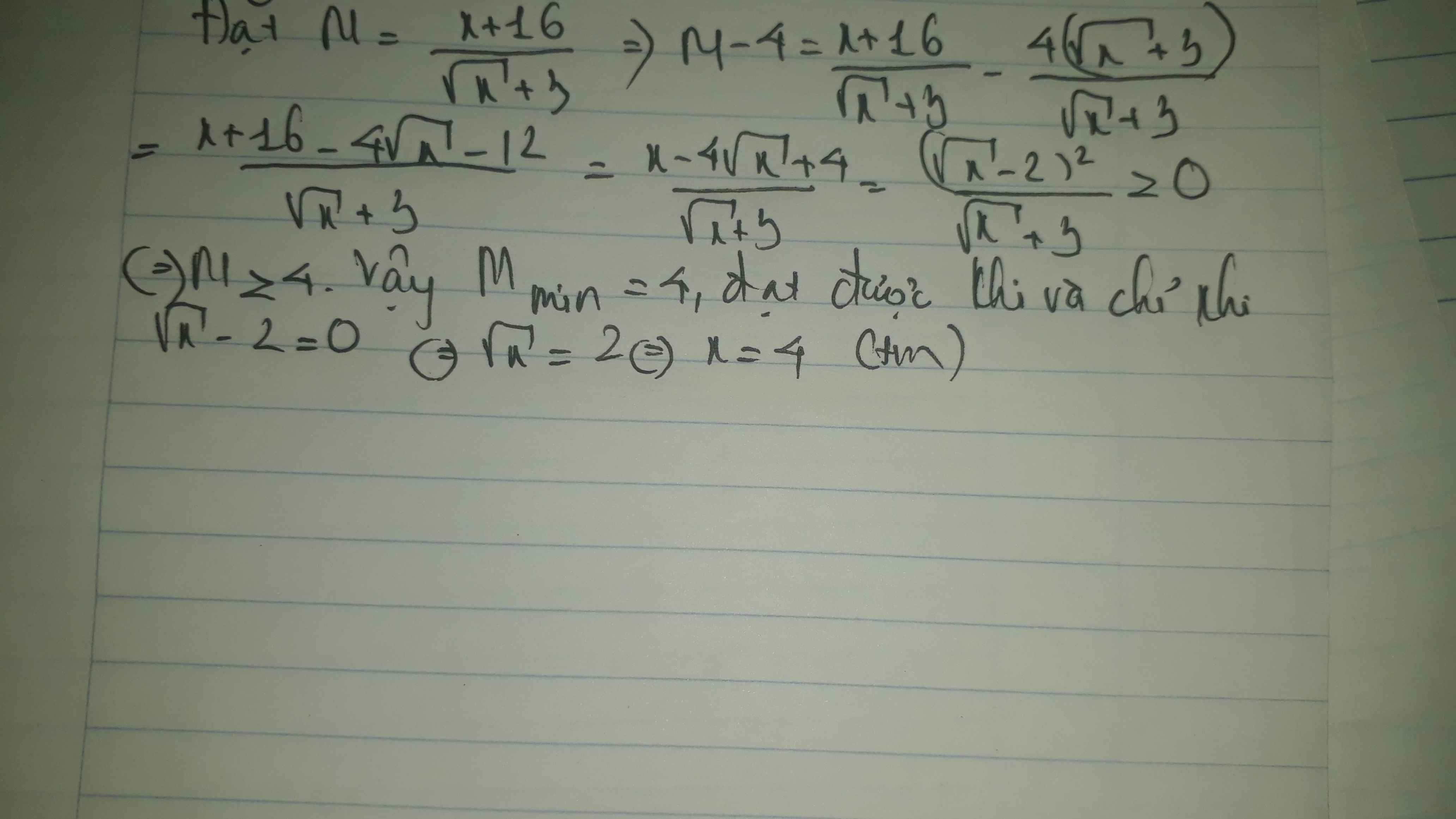
ĐK: `x-4>=0 <=>x>=4`
`\sqrt(x-4)>=0 forall x`
`<=>\sqrt(x-4)-2>=-2`
`=> (\sqrt(x-4)-2)_(min) =-2<=> x=4`