Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
TXĐ: D = R
+ y' = 2cos2x – 1;
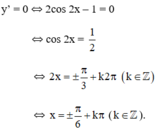
+ y" = -4.sin2x
⇒ 
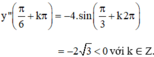
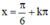(k ∈ Z) là các điểm cực đại của hàm số.
⇒ 
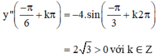
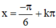(k ∈ Z) là các điểm cực tiểu của hàm số.
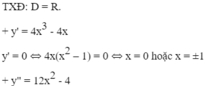
y"(0) = -4 < 0 ⇒ x = 0 là điểm cực đại của hàm số.
y"(1) = 8 > 0 ⇒ x = 1 là điểm cực tiểu của hàm số.
y"(-1) = 8 > 0 ⇒ x = -1 là điểm cực tiểu của hàm số.
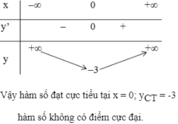
TXĐ: D = R
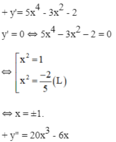
y"(-1) = -20 + 6 = -14 < 0
⇒ x = -1 là điểm cực đại của hàm số.
y"(1) = 20 – 6 = 14 > 0
⇒ x = 1 là điểm cực tiểu của hàm số.
TXĐ: D = R \ {0}
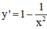
y' = 0 ⇔ x = ±1
Bảng biến thiên:
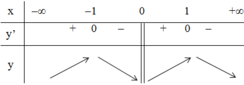
Vậy hàm số đạt cực đại tại x = -1; yCĐ = -2;
hàm số đạt cực tiểu tại x = 1; yCT = 2.
TXĐ: D = R
y' = 6x2 + 6x - 36
y' = 0 ⇔ x = -3 hoặc x = 2
Bảng biến thiên:
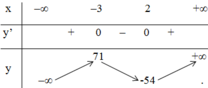
Kết luận :
Hàm số đạt cực đại tại x = -3 ; yCĐ = 71
Hàm số đạt cực tiểu tại x = 2; yCT = -54.
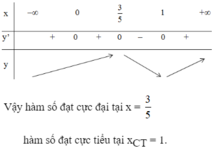
1. TXĐ: D = R
2. f’(x) = 3x^2 – 3. Cho f’(x) = 0 ⇔ x = 1 hoặc x = -1.
3. Ta có bảng biến thiên:
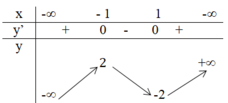
Hàm số đạt cực đại tại x = -1 và giá trị cực đại là 2
Hàm số đạt cực tiểu tại x = 1 và giá trị cực tiểu là -2.
\(y'=cosx-sinx=0\)
\(\Leftrightarrow x=\frac{\pi}{4}+k\pi\)
\(y''=-sinx-cosx\)
\(y''\left(\frac{\pi}{4}+k2\pi\right)=-\sqrt{2}< 0\)
\(y''\left(\frac{\pi}{4}+\left(2k+1\right)\pi\right)=\sqrt{2}>0\)
\(\Rightarrow\) Hàm đạt cực đạt tại những điểm thỏa mãn \(x=\frac{\pi}{4}+k2\pi\)
Hàm đạt cực tiểu tại những điểm \(x=\frac{5\pi}{4}+k2\pi\)
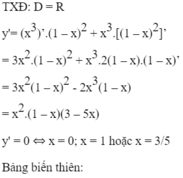
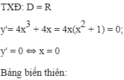
TXĐ: D = R
+ y’ = cos x – sin x.
+ y’’ = -sin x – cos x =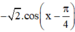
⇒
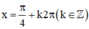là các điểm cực đại của hàm số.
⇒
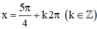là các điểm cực tiểu của hàm số.