Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

c, \(C=\left(2\sqrt{3}-5\sqrt{27}+4\sqrt{12}\right):\sqrt{3}\)
<=> \(C=\left(2\sqrt{3}-15\sqrt{3}+8\sqrt{3}\right):\sqrt{3}\)
<=> \(C=-5\sqrt{3}:\sqrt{3}=-5\)
e. \(\left(\sqrt{3-\sqrt{5}}+\sqrt{3+\sqrt{5}}\right)^2\)
\(=3-\sqrt{5}+3+\sqrt{5}+2\sqrt{\left(3-\sqrt{5}\right)\left(3+\sqrt{5}\right)}\)
\(=6+2\sqrt{9-5}\)
\(=6+4=10\)
b. \(\left(\sqrt{3}+2\right)^2-\sqrt{75}\)
\(=3+4\sqrt{3}+4-5\sqrt{3}\)
\(=7-\sqrt{3}\)
d. \(\left(1+\sqrt{3}-\sqrt{2}\right)\left(1+\sqrt{3}+\sqrt{2}\right)\)
\(=\left(1+\sqrt{3}\right)^2-2\)
\(=1+2\sqrt{3}+3-2\)
\(=2+2\sqrt{3}\)
f. \(\sqrt{\left(\sqrt{3}+2\right)^2}-\sqrt{\left(\sqrt{3}-2\right)^2}\)
\(=\left|\sqrt{3}+2\right|-\left|\sqrt{3}-2\right|\)
\(=\sqrt{3}+2-2+\sqrt{3}\)
\(=2\sqrt{3}\)
c: Ta có: \(C=\left(2\sqrt{3}-5\sqrt{27}+4\sqrt{12}\right):\sqrt{3}\)
\(=\left(2\sqrt{3}-5\cdot3\sqrt{3}+4\cdot2\sqrt{3}\right):\sqrt{3}\)
\(=2-15+8=-5\)
d: Ta có: \(D=\left(\sqrt{3-\sqrt{5}}+\sqrt{3+\sqrt{5}}\right)^2\)
\(=3-\sqrt{5}+3+\sqrt{5}+2\cdot\sqrt{\left(3-\sqrt{5}\right)\left(3+\sqrt{5}\right)}\)
\(=6+2\cdot2=10\)


2:
a: AC=căn 5^2-3^2=4cm
sin B=AC/BC=4/5
cos B=AB/BC=3/5
tan B=4/5:3/5=4/3
cot B=1:4/3=3/4
b: AB=căn 13^2-12^2=5cm
sin B=AC/BC=12/13
cos B=AB/BC=5/13
tan B=12/13:5/13=12/5
cot C=1:12/5=5/12
c: BC=căn 4^2+3^2=5cm
sin B=AC/BC=4/5
cos B=AB/BC=3/5
tan B=4/5:3/5=4/3
cot B=1:4/3=3/4

b) Ta có: \(9x^4+8x^2-1=0\)
\(\Leftrightarrow9x^4+9x^2-x^2-1=0\)
\(\Leftrightarrow9x^2\left(x^2+1\right)-\left(x^2+1\right)=0\)
\(\Leftrightarrow\left(x^2+1\right)\left(9x^2-1\right)=0\)
mà \(x^2+1>0\forall x\)
nên \(9x^2-1=0\)
\(\Leftrightarrow9x^2=1\)
\(\Leftrightarrow x^2=\dfrac{1}{9}\)
hay \(x\in\left\{\dfrac{1}{3};-\dfrac{1}{3}\right\}\)
Vậy: \(S=\left\{\dfrac{1}{3};-\dfrac{1}{3}\right\}\)

a: Để hàm số này làm hàm số bậc nhất thì 2m-3<>0
hay m<>3/2

b: Xét ΔABE vuông tại A có AH là đường cao ứng với cạnh huyền BE
nên \(BH\cdot BE=AB^2\left(1\right)\)
Xét ΔABC vuông tại B có BH là đường cao ứng với cạnh huyền AC
nên \(AH\cdot AC=AB^2\left(2\right)\)
Từ (1) và (2) suy ra \(BH\cdot BE=AH\cdot AC\)
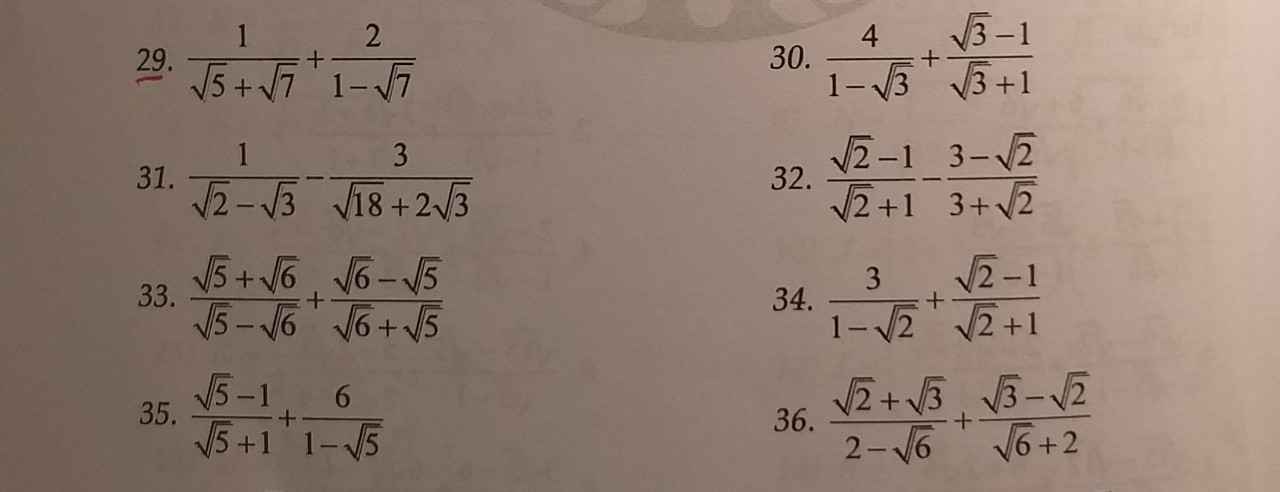
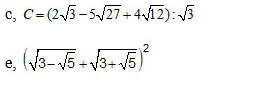
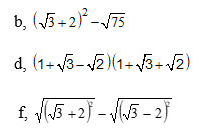 các bạn giải hộ mik mấy câu này vs mik đag cần gấp
các bạn giải hộ mik mấy câu này vs mik đag cần gấp
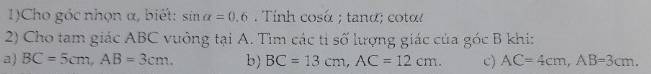
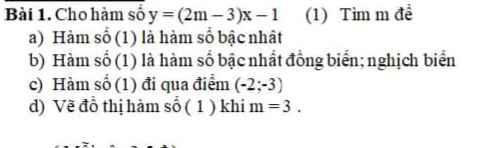

29: Ta có: \(\dfrac{1}{\sqrt{7}+\sqrt{5}}+\dfrac{2}{1-\sqrt{7}}\)
\(=\dfrac{\sqrt{7}-\sqrt{5}}{2}-\dfrac{2\sqrt{7}-2}{6}\)
\(=\dfrac{3\sqrt{7}-3\sqrt{5}-2\sqrt{7}+2}{6}\)
\(=\dfrac{-3\sqrt{5}-2}{6}\)
30: Ta có: \(\dfrac{4}{1-\sqrt{3}}+\dfrac{\sqrt{3}-1}{\sqrt{3}+1}\)
\(=\dfrac{-4\sqrt{3}-4}{2}+\dfrac{4-2\sqrt{3}}{2}\)
\(=\dfrac{-4\sqrt{3}-4+4-2\sqrt{3}}{2}=-3\sqrt{3}\)
31: Ta có: \(\dfrac{1}{\sqrt{2}-\sqrt{3}}-\dfrac{3}{\sqrt{18}+2\sqrt{3}}\)
\(=-\sqrt{3}-\sqrt{2}-\dfrac{3}{3\sqrt{2}+2\sqrt{3}}\)
\(=-\sqrt{3}-\sqrt{2}-\dfrac{9\sqrt{2}-6\sqrt{3}}{6}\)
\(=\dfrac{-6\sqrt{3}-6\sqrt{2}-9\sqrt{2}+6\sqrt{3}}{6}=\dfrac{-15\sqrt{2}}{6}\)
\(=\dfrac{-5\sqrt{2}}{2}\)
29.
\(=\frac{\sqrt{7}-\sqrt{5}}{(\sqrt{7}-\sqrt{5})(\sqrt{7}+\sqrt{5})}+\frac{2(1+\sqrt{7})}{(1-\sqrt{7})(1+\sqrt{7})}\)
\(=\frac{\sqrt{7}-\sqrt{5}}{7-5}+\frac{2(1+\sqrt{7})}{1-7}=\frac{\sqrt{7}-\sqrt{5}}{2}-\frac{1+\sqrt{7}}{3}=\frac{\sqrt{7}-3\sqrt{5}-2}{6}\)