
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.


\(\dfrac{x}{6}=\dfrac{7}{4}\Rightarrow x=\dfrac{6\cdot7}{4}=\dfrac{21}{2}\\ \dfrac{3}{x}=\dfrac{21}{17}\Rightarrow x=\dfrac{3\cdot17}{21}=\dfrac{17}{7}\)

Câu 3:
a: Áp dụng tính chất của dãy tỉ số bằng nhau, ta được:
\(\dfrac{x}{3}=\dfrac{y}{2}=\dfrac{x+y}{3+2}=\dfrac{90}{5}=18\)
Do đó: x=54; y=36

\(a,=\dfrac{1}{64}\cdot64=1\\ b,=\left(\dfrac{3}{4}\cdot\dfrac{4}{3}\right)^3+\dfrac{1}{3}=1+\dfrac{1}{3}=\dfrac{4}{3}\\ c,=\left(\dfrac{3}{2}\right)^2=\dfrac{9}{4}\\ d,=\dfrac{1}{2^{2004}}\cdot9^{1002}\\ =\dfrac{9^{1002}}{4^{1002}}=\left(\dfrac{3}{2}\right)^{1002}\)
a. (0,125)2 . 64
= \(\dfrac{1}{64}.\dfrac{64}{1}\)
= \(\dfrac{1.1}{1.1}=1\)

b: Ta có: \(47\dfrac{1}{9}:\left(-\dfrac{5}{2}\right)-27\dfrac{1}{9}:\left(-\dfrac{5}{2}\right)\)
\(=\left(47+\dfrac{1}{9}\right)\cdot\dfrac{-2}{5}-\left(27+\dfrac{1}{9}\right)\cdot\dfrac{-2}{5}\)
\(=20\cdot\dfrac{-2}{5}\)
=-8






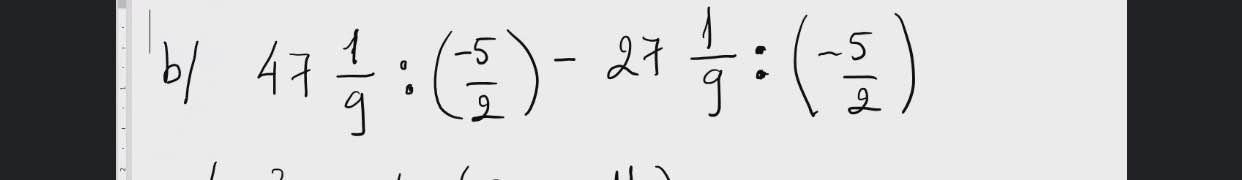
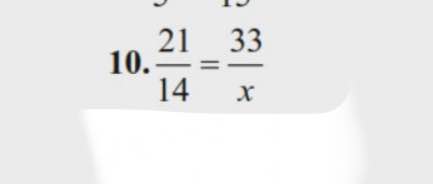
ta có P(x)=x^2+ax+b ; Q(x)=x^2+cx+d
ta có x1 và x2 là nghiêm của P(x)Dán
nên \(x_1^2+ax_1+b=0;x_2^2+ax_2+b=0\)
\(\Rightarrow x_1^2=-ax_1-b\) và \(x_2^2=-ax_2-b\) (1)
Ta có x1,x2 là nghiêm của Q(x)
nên \(x_1^2+cx_1+d=0;x_2^2+cx_2+d=0\)
\(\Rightarrow x_1^2=-cx_1-d\)và \(x_2^2=-cx_2-d\) (2)
Từ (1) và (2) suy ra \(-ax_1-b=-cx_1-d\\ -ax_2-b=-cx_2-d\)
Do đó \(ax_1+b=cx_1+d\\ ax_2+b=+cx_2+d\)
Suy ra\(x_1^2+ax_1+b=x^2_1+cx_1+d\\ x^2_2+ax_2+b=x^2_2+cx_2+d\)
Nên P(x)=Q(x)
Q(x) =x2 +ax + b
P(x) = x2 +cx + d
Vì x1;x2 đều là nghiệm của P(x); Q(x)
=>x1;x2 là nghiệm của : P(x) - Q(x)=(c-a)x +(d-b)
=> PT: (c-a)x +(d-b) =0 có 2 nghiệm x1;x2
=>\(\left\{{}\begin{matrix}c-a=0\\d-b=0\end{matrix}\right.\Leftrightarrow\left\{{}\begin{matrix}a=c\\b=d\end{matrix}\right.\)
Nên => P(x) = Q(x) dpcm