K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Các câu hỏi dưới đây có thể giống với câu hỏi trên
13 tháng 11 2021
2: Thay x=1 và y=-4 vào (d), ta được:
2m+2=-4
hay m=-3
NL
1
21 tháng 10 2021
\(d,ĐK:x\ge1\\ PT\Leftrightarrow\sqrt{x-1}=2+\sqrt{x+1}\\ \Leftrightarrow x-1=2+x+1+4\sqrt{x+1}\\ \Leftrightarrow4\sqrt{x+1}=-4\Leftrightarrow x\in\varnothing\left(4\sqrt{x+1}\ge0\right)\\ g,ĐK:x\ge\dfrac{1}{2}\\ PT\Leftrightarrow x+\sqrt{2x-1}+x-\sqrt{2x-1}+2\sqrt{\left(x+\sqrt{2x-1}\right)\left(x-\sqrt{2x-1}\right)}=2\\ \Leftrightarrow2x+2\sqrt{x^2-2x+1}=2\\ \Leftrightarrow\sqrt{\left(x-1\right)^2}=\dfrac{2-2x}{2}=1-x\\ \Leftrightarrow\left|x-1\right|=1-x\\ \Leftrightarrow\left[{}\begin{matrix}x-1=1-x\left(x\ge1\right)\\x-1=x-1\left(x< 1\right)\end{matrix}\right.\Leftrightarrow\left[{}\begin{matrix}x=1\left(tm\right)\\x\in R\end{matrix}\right.\)
A
, mình đang cần giải gấp. Cảm ơn mn nhiều.
1
3 tháng 9 2021
Bài 3:
a: Gọi OK là khoảng cách từ O đến AB
Suy ra: K là trung điểm của AB
hay \(AK=BK=\dfrac{AB}{2}=\dfrac{8}{2}=4\left(cm\right)\)
Áp dụng định lí Pytago vào ΔOKA vuông tại K, ta được:
\(OA^2=OK^2+KA^2\)
hay OK=3(cm)
NT
1
7 tháng 12 2021
Xét ΔOHA vuông tại H và ΔOKA vuông tại K có
OA chung
OH=OK
Do đó: ΔOHA=ΔOKA
Suy ra: AH=AK
hay AB=AC
A
0
A
1
26 tháng 9 2021
c: \(f\left(5-2\sqrt{3}\right)=f\left(2\right)\)
\(\Leftrightarrow\sqrt{4-2\sqrt{3}}+m\left(5-2\sqrt{3}\right)+2=\sqrt{2-1}+2m+2\)
\(\Leftrightarrow\sqrt{3}+1+m\left(5-2\sqrt{3}\right)=2m+3\)
\(\Leftrightarrow m\left(3-2\sqrt{3}\right)=2-\sqrt{3}\)
hay \(m=-\dfrac{\sqrt{3}}{3}\)
NL
1
6 tháng 12 2021
Bài 2:
Thay x=3 và y=-5 vào (d), ta được:
b-6=-5
hay b=1
LD
6 tháng 4 2023
\(x^2-2\left(m-2\right)x+m^2+2m-3=0\left(1\right)\)
Để phương trình có hai nghiệm phân biệt thì Δ' > 0
\(\Rightarrow\left(m-2\right)^2-m^2-2m+3>0\Leftrightarrow m^2-4m+4-m^2-2m+3>0\Leftrightarrow-6m+7>0\Leftrightarrow m< \dfrac{7}{6}\)\)
Theo viét : \(\(\left\{{}\begin{matrix}x_1+x_2=2\left(m-2\right)\\x_1x_2=m^2+2m-3\end{matrix}\right.\)\)
Lại có :\( \dfrac{1}{x_1}+\dfrac{1}{x_2}=\dfrac{x_1+x_2}{5}\)
\(\Leftrightarrow\dfrac{x_1+x_2}{x_1x_2}=\dfrac{x_1+x_2}{5}\)
\(\Rightarrow\left(x_1+x_2\right)\left(x_1x_2\right)=5\left(x_1+x_2\right)\)
\(\Leftrightarrow\left(2m-4\right)\left(m^2+2m-3\right)=5\left(2m-4\right)\)
\(\Leftrightarrow2m^3+4m^2-6m-4m^2-8m+12=10m-20\)
\(\Leftrightarrow2m^3-24m+32=0\) \(\Leftrightarrow\left[{}\begin{matrix}m=-4\left(n\right)\\m=2\left(l\right)\end{matrix}\right.\)
Vậy \(m=-4\) thì thỏa điều kiện
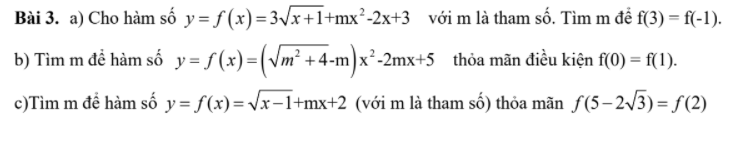
a: Khi m=2 thì (1) se là x^2-2x-3=0
=>x=3 hoặc x=-1
b: Vì a*c<0 nên (1) luôn có hai nghiệm phân biệt