ai giúp em câu này với
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Các câu hỏi dưới đây có thể giống với câu hỏi trên
ai giúp em câu này với
24 tháng 10 2021
\(A=\sqrt{\dfrac{3\sqrt{5}-1}{3+2\sqrt{5}}}-\sqrt{\dfrac{\sqrt{5}-1}{\sqrt{5}-2}}\)
\(=\sqrt{3-\sqrt{5}}-\sqrt{3+\sqrt{5}}\)
\(=\dfrac{\sqrt{5}-1-\sqrt{5}-1}{\sqrt{2}}\)
\(=-\sqrt{2}\)
NV
Nguyễn Việt Lâm
Giáo viên
24 tháng 1 2022
Chắc đề đúng là \(\dfrac{1}{4+1^4}+\dfrac{3}{4+3^4}+...\)
- Với \(n=1\) đẳng thức đúng
- Giả sử đẳng thức cũng đúng với \(n=k>1\) hay:
\(\dfrac{1}{4+1^4}+\dfrac{3}{4+3^4}+...+\dfrac{2k-1}{4+\left(2k-1\right)^4}=\dfrac{k^2}{4k^2+1}\)
- Ta cần chứng minh nó cũng đúng với \(n=k+1\) hay:
\(\dfrac{1}{4+1^4}+\dfrac{3}{4+3^4}+...+\dfrac{2k-1}{4+\left(2k-1\right)^4}+\dfrac{2k+1}{4+\left(2k+1\right)^4}=\dfrac{\left(k+1\right)^2}{4\left(k+1\right)^2+1}\)
Thật vậy, ta có:
\(\dfrac{1}{4+1^4}+\dfrac{3}{4+3^4}+...+\dfrac{2k-1}{4+\left(2k-1\right)^4}+\dfrac{2k+1}{4+\left(2k+1\right)^4}=\dfrac{k^2}{4k^2+1}+\dfrac{2k+1}{4+\left(2k+1\right)^4}\)
\(=\dfrac{k^2}{4k^2+1}+\dfrac{2k+1}{\left(2k+1\right)^4+4\left(2k+1\right)^2+4-4\left(2k+1\right)^2}=\dfrac{k^2}{4k^2+1}+\dfrac{2k+1}{\left(4k^2+4k+3\right)^2-\left(4k+2\right)^2}\)
\(=\dfrac{k^2}{4k^2+1}+\dfrac{2k+1}{\left(4k^2+1\right)\left(4k^2+8k+5\right)}=\dfrac{k^2\left(4k^2+8k+5\right)+2k+1}{\left(4k^2+1\right)\left(4k^2+8k+5\right)}\)
\(=\dfrac{\left(k+1\right)^2\left(4k^2+1\right)}{\left(4k^2+1\right)\left(4k^2+8k+5\right)}=\dfrac{\left(k+1\right)^2}{4k^2+8k+5}=\dfrac{\left(k+1\right)^2}{4\left(k+1\right)^2+1}\) (đpcm)
21 tháng 9 2021
\(=\left(6\sqrt{2}-6\sqrt{2}+6\sqrt{2}\right):\sqrt{2}=6\sqrt{2}:\sqrt{2}=6\)
23 tháng 1 2022
a, thay x=25 vào A ta có:
\(A=\dfrac{\sqrt{x}}{\sqrt{x}-1}=\dfrac{\sqrt{25}}{\sqrt{25}-1}=\dfrac{5}{5-1}=\dfrac{5}{4}\)
b, \(P=\dfrac{\sqrt{x}}{\sqrt{x}-1}\left(\dfrac{3x+3}{x\sqrt{x}-1}-\dfrac{2}{\sqrt{x}-1}\right)\)
\(\Rightarrow P=\dfrac{\sqrt{x}}{\sqrt{x}-1}\left(\dfrac{3x+3}{\sqrt{x^3}-1}-\dfrac{2\left(x+\sqrt{x}+1\right)}{\left(\sqrt{x}-1\right)\left(x+\sqrt{x}+1\right)}\right)\)
\(\Rightarrow P=\dfrac{\sqrt{x}}{\sqrt{x}-1}\left(\dfrac{3x+3}{\left(\sqrt{x}-1\right)\left(x+\sqrt{x}+1\right)}-\dfrac{2x+2\sqrt{x}+2}{\left(\sqrt{x}-1\right)\left(x+\sqrt{x}+1\right)}\right)\)
\(\Rightarrow P=\dfrac{\sqrt{x}}{\sqrt{x}-1}.\dfrac{3x+3-2x-2\sqrt{x}-2}{\left(\sqrt{x}-1\right)\left(x+\sqrt{x}+1\right)}\)
\(\Rightarrow P=\dfrac{\sqrt{x}\left(x-2\sqrt{x}+1\right)}{\left(\sqrt{x}-1\right)^2\left(x+\sqrt{x}+1\right)}\)
\(\Rightarrow P=\dfrac{\sqrt{x}\left(\sqrt{x}-1\right)^2}{\left(\sqrt{x}-1\right)^2\left(x+\sqrt{x}+1\right)}\)
\(\Rightarrow P=\dfrac{\sqrt{x}}{x+\sqrt{x}+1}\)
22 tháng 9 2021
\(=2\sqrt{3}-10\sqrt{3}-\sqrt{3}+\dfrac{5\sqrt{3}}{2}=\dfrac{5\sqrt{3}}{2}-9\sqrt{3}=\dfrac{5\sqrt{3}-18\sqrt{3}}{2}=\dfrac{-13\sqrt{3}}{2}\)
22 tháng 9 2021
\(=\dfrac{1}{2}.4\sqrt{3}-2.5\sqrt{3}-\sqrt{3}+5.\dfrac{\sqrt{3}}{2}\)
\(=2\sqrt{3}-10\sqrt{3}-\sqrt{3}+\dfrac{5\sqrt{3}}{2}\)
\(=-9\sqrt{3}+\dfrac{5\sqrt{3}}{2}=\dfrac{-18\sqrt{3}+5\sqrt{3}}{2}=-\dfrac{13\sqrt{3}}{2}\)
N
23 tháng 1 2022
Giải hpt:
Đặt: \(\left[{}\begin{matrix}\sqrt{x-1}=a\\y+1=b\end{matrix}\right.\)
Ta có: \(\left\{{}\begin{matrix}3a-2b=-1\\5a-9b=-13\end{matrix}\right.< =>\left\{{}\begin{matrix}15a-10b=-5\\15a-27b=-39\end{matrix}\right.< =>\left\{{}\begin{matrix}b=2\\15a-27\cdot2=-39\end{matrix}\right.< =>\left\{{}\begin{matrix}b=2\\a=1\end{matrix}\right.\)
Thay: \(\left[{}\begin{matrix}\sqrt{x-1}=1\\y+1=2\end{matrix}\right.< =>\left[{}\begin{matrix}x=2\\y=1\end{matrix}\right.\)
SE
1
NV
Nguyễn Việt Lâm
Giáo viên
12 tháng 4 2021
\(A=\sqrt{2a\left(b+1\right)}+\sqrt{2b\left(c+1\right)}+\sqrt{2c\left(a+1\right)}\)
\(A=\dfrac{1}{\sqrt{2}}\sqrt{4a\left(b+1\right)}+\dfrac{1}{\sqrt{2}}\sqrt{4b\left(c+1\right)}+\dfrac{1}{\sqrt{2}}\sqrt{4c\left(a+1\right)}\)
\(A\le\dfrac{1}{2\sqrt{2}}\left(4a+b+1\right)+\dfrac{1}{2\sqrt{2}}\left(4b+c+1\right)+\dfrac{1}{2\sqrt{2}}\left(4c+a+1\right)\)
\(A\le\dfrac{1}{2\sqrt{2}}\left[5\left(a+b+c\right)+3\right]=2\sqrt{2}\)
\(A_{max}=2\sqrt{2}\) khi \(a=b=c=\dfrac{1}{3}\)
2 tháng 12 2021
\(1,\left\{{}\begin{matrix}3x-y=5\\5x+2y=23\end{matrix}\right.\\ \Leftrightarrow\left\{{}\begin{matrix}y=3x-5\\5x+2\left(3x-5\right)=23\end{matrix}\right.\\ \Leftrightarrow\left\{{}\begin{matrix}y=3x-5\\5x+6x-10=23\end{matrix}\right.\\ \Leftrightarrow\left\{{}\begin{matrix}y=3x-5\\11x=33\end{matrix}\right.\\ \Leftrightarrow\left\{{}\begin{matrix}y=3.3-5\\x=3\end{matrix}\right.\\ \Leftrightarrow\left\{{}\begin{matrix}y=4\\x=3\end{matrix}\right.\)
\(2,\left\{{}\begin{matrix}5x-4y=3\\2x+y=4\end{matrix}\right.\\ \Leftrightarrow\left\{{}\begin{matrix}5x-4\left(4-2x\right)=3\\y=4-2x\end{matrix}\right.\\ \Leftrightarrow\left\{{}\begin{matrix}5x-16+8x=3\\y=4-2x\end{matrix}\right.\\ \Leftrightarrow\left\{{}\begin{matrix}13x=19\\y=4-2x\end{matrix}\right.\\ \Leftrightarrow\left\{{}\begin{matrix}x=\dfrac{19}{13}\\y=4-2.\dfrac{19}{13}\end{matrix}\right.\\ \Leftrightarrow\left\{{}\begin{matrix}x=\dfrac{19}{13}\\y=\dfrac{14}{13}\end{matrix}\right.\)
27 tháng 12 2021
\(b,\Leftrightarrow\left\{{}\begin{matrix}m+1=3\\m-3\ne-3\end{matrix}\right.\Leftrightarrow m=2\\ c,\text{PT giao Ox tại hoành độ 3: }\\ x=-3;y=0\Leftrightarrow\left(m+1\right)\left(-3\right)+m-3=0\\ \Leftrightarrow-2m-6=0\Leftrightarrow m=-3\)
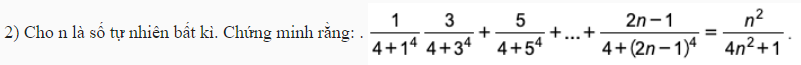
\(\sqrt{\dfrac{2}{2-\sqrt{3}}}-\sqrt{\dfrac{2}{2+\sqrt{3}}}=\dfrac{\sqrt{4+2\sqrt{3}}-\sqrt{4-2\sqrt{3}}}{\sqrt{\left(2-\sqrt{3}\right)\left(2+\sqrt{3}\right)}}=\dfrac{\sqrt{\left(\sqrt{3}+1\right)^2}-\sqrt{\left(\sqrt{3}-1\right)^2}}{\sqrt{4-3}}\)
\(=\sqrt{3}+1-\sqrt{3}+1=2\)
em cảm ơn ạ