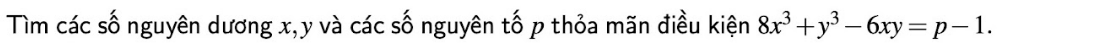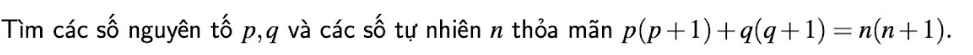K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Các câu hỏi dưới đây có thể giống với câu hỏi trên
NV
1
25 tháng 11 2021
Xét tứ giác FOGD có ^F=^D=^G=900
⇒FOGD là hình chữ nhật
Vì ABCD là hình vuông ⇒AC=BD ,O là trung điểm của AC , BD
⇒OA=OD=OG
Xét △AOD có OA=OD(cmt)
⇒△AOD cân tại O có OF là đường cao ⇔OF đồng thời là đường trung tuyến ứng với cạnh AD⇒AF=FD=\(\dfrac{1}{2}\)AD
tương tự ta có △ODC cân tại O⇒DG=GC=\(\dfrac{1}{2}\)DC
⇔DF=DG=AF=GC
Xét hình chữ nhật FOGD có DF=DG(cmt)
⇒FOGD là hình vuông
NV
0
NV
1
6 tháng 11 2021
Bài 15:
\(P=\dfrac{x+y-1}{x\left(x+y\right)}+\dfrac{x-y}{2xy}\cdot\dfrac{xy+y^2+xy-y^2}{x\left(x-y\right)\left(x+y\right)}\)
\(=\dfrac{1}{x}\)
9 tháng 12 2015
Số học sinh nam là:
(x + y) : 2 = ?
Số học sinh nữ là:
x - ? = ?
Đáp số : ...
TN
1
LN
11 tháng 11 2015
\(x^2+y^2-x+6y+10\)
=>\(\left(x^2-2\times\frac{1}{2}x+\frac{1}{4}\right)+\left(y^2+6y+9\right)+\frac{3}{4}\)
=>\(\left(x-\frac{1}{2}\right)^2+\left(y+3\right)^2+\frac{3}{4}\)
Vì \(\left(x-\frac{1}{2}\right)^2\ge0\) (Với mọi x)
\(\left(y+3\right)^2\ge0\) (Với mọi x)
=>\(\left(x-\frac{1}{2}\right)^2+\left(y+3\right)^2+\frac{3}{4}\ge\frac{3}{4}\) (Với mọi x)
Dấu "=" xảy ra <=>\(\left(x-\frac{1}{2}\right)^2+\left(y+3\right)^2=0\)
=>\(x=\frac{1}{2}\) và \(y=-3\)
Vậy GTNN của bt =3 khi và chỉ khi x=\(\frac{1}{2}\) và \(y=-3\)
LM
ai giải giúp em mấy bài toán này vs ạ giải chi tiết giúp em ạ
1
10 tháng 11 2021
\(1,\\ a,=6x^4y^4-x^3y^3+\dfrac{1}{2}x^4y^2\\ b,=4x^3+5x^2-8x^2-10x+12x+15\\ =4x^3-3x^2+2x+15\\ 2,\\ a,=7\left(x^2-6x+9\right)=7\left(x-3\right)^2\\ b,=\left(x-y\right)^2-36=\left(x-y-6\right)\left(x-y+6\right)\\ 3,\\ \Leftrightarrow x\left(x^2-0,36\right)=0\\ \Leftrightarrow x\left(x-0,6\right)\left(x+0,6\right)=0\\ \Leftrightarrow\left[{}\begin{matrix}x=0\\x=0,6\\x=-0,6\end{matrix}\right.\)
EG
cd
4
7 tháng 10 2021
a: Xét ΔBDC có
M là trung điểm của BC
H là trung điểm của DC
Do đó: MH là đường trung bình của ΔBDC
Suy ra: MH//DB
