
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.



c) C = \(\dfrac{4}{\sqrt{3}+1} - \dfrac{5}{\sqrt{3}-2} + \dfrac{6}{\sqrt{3}-3}\)
⇔ C = \(\dfrac{4(\sqrt{3}-1)}{2} - \dfrac{5(\sqrt{3}-2)}{-1} - \dfrac{6(\sqrt{3}+3)}{-6}\)
⇔ C = \(2\sqrt{3} -2 + 5\sqrt{3} + 10 - \sqrt{3} - 3\)
⇔ C = \(6\sqrt{3} + 5\)


Lời giải:
Áp dụng định lý Viet đối với pt $x^2+3x-7=0$ ta có:
$x_1+x_2=-3$
$x_1x_2=-7$
Khi đó:
$\frac{1}{x_1-1}+\frac{1}{x_2-1}=\frac{x_2-1+x_1-1}{(x_1-1)(x_2-1)}$
$=\frac{(x_1+x_2)-2}{x_1x_2-(x_1+x_2)+1}=\frac{-3-2}{-7-(-3)+1}=\frac{5}{3}$
$\frac{1}{x_1-1}.\frac{1}{x_2-1}=\frac{1}{(x_1-1)(x_2-1)}=\frac{1}{x_1x_2-(x_1+x_2)+1}=\frac{1}{-7-(-3)+1}=\frac{-1}{3}$
Khi đó áp dụng định lý Viet đảo, $\frac{1}{x_1-1}, \frac{1}{x_2-1}$ là nghiệm của pt:
$x^2-\frac{5}{3}x-\frac{1}{3}=0$
Lời giải:
Áp dụng định lý Viet đối với pt $x^2+3x-7=0$ ta có:
$x_1+x_2=-3$
$x_1x_2=-7$
Khi đó:
$\frac{1}{x_1-1}+\frac{1}{x_2-1}=\frac{x_2-1+x_1-1}{(x_1-1)(x_2-1)}$
$=\frac{(x_1+x_2)-2}{x_1x_2-(x_1+x_2)+1}=\frac{-3-2}{-7-(-3)+1}=\frac{5}{3}$
$\frac{1}{x_1-1}.\frac{1}{x_2-1}=\frac{1}{(x_1-1)(x_2-1)}=\frac{1}{x_1x_2-(x_1+x_2)+1}=\frac{1}{-7-(-3)+1}=\frac{-1}{3}$
Khi đó áp dụng định lý Viet đảo, $\frac{1}{x_1-1}, \frac{1}{x_2-1}$ là nghiệm của pt:
$x^2-\frac{5}{3}x-\frac{1}{3}=0$

\(3x^4+4x^3-3x^2-2x+1=0\)
\(\Leftrightarrow3x^4+x^3-x^2+3x^3+x^2-x-3x^2-x+1=0\)
\(\Leftrightarrow x^2\left(3x^2+x-1\right)+x\left(3x^2+x-1\right)-\left(3x^2+x-1\right)=0\)
\(\Leftrightarrow\left(x^2+x-1\right)\left(3x^2+x-1\right)=0\)
\(\Leftrightarrow\orbr{\begin{cases}x^2+x-1=0\left(1\right)\\3x^2+x-1=0\left(2\right)\end{cases}}\)
- \(\Delta_{\left(1\right)}=1^2-\left(-4\left(1.1\right)\right)=5\)
\(\Leftrightarrow x_{1,2}=\frac{-1\pm\sqrt{5}}{2}\left(tm\right)\)
- \(\Delta_{\left(2\right)}=1^2-\left(-4\left(3.1\right)\right)=13\)
\(x_{1,2}=\frac{-1\pm\sqrt{13}}{6}\left(tm\right)\)

2x2 - ( m + 4 )x + m = 0
Δ = b2 - 4ac = ( m + 4 )2 - 8m = m2 + 8m + 16 - 8m = m2 + 16
Vì m2 + 16 ≥ 16 > 0 ∀ m => Δ ≥ 16 > 0
Vậy phương trình luôn có nghiệm ( đpcm )

\(b,\Leftrightarrow\left\{{}\begin{matrix}m+1=3\\m-3\ne-3\end{matrix}\right.\Leftrightarrow m=2\\ c,\text{PT giao Ox tại hoành độ 3: }\\ x=-3;y=0\Leftrightarrow\left(m+1\right)\left(-3\right)+m-3=0\\ \Leftrightarrow-2m-6=0\Leftrightarrow m=-3\)




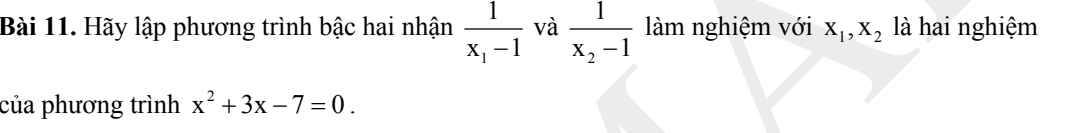


1) ĐKXĐ: \(x\ge-5\)
\(pt\Leftrightarrow x+5=9\Leftrightarrow x=9-5=4\left(tm\right)\)
2) ĐKXĐ: \(x\ge3\)
\(pt\Leftrightarrow3\sqrt{x-3}-\sqrt{x-3}=6\)
\(\Leftrightarrow2\sqrt{x-3}=6\Leftrightarrow\sqrt{x-3}=3\)
\(\Leftrightarrow x-3=9\Leftrightarrow x=12\left(tm\right)\)
3) ĐKXĐ: \(x\ge-1\)
\(pt\Leftrightarrow\sqrt{\left(x+1\right)^2}-2\sqrt{x+1}=0\)
\(\Leftrightarrow x+1-2\sqrt{x+1}=0\)
\(\Leftrightarrow\sqrt{x+1}\left(\sqrt{x+1}-2\right)=0\)
\(\Leftrightarrow\left[{}\begin{matrix}x+1=0\\x+1=4\end{matrix}\right.\)\(\Leftrightarrow\left[{}\begin{matrix}x=-1\left(tm\right)\\x=3\left(tm\right)\end{matrix}\right.\)
tui uk.......u...a