Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

Việc gọi ẩn ko ảnh hưởng gì tới kết quả bài toán cả, cứ thoải mái đi

Đặt \(\int f\left(x\right)dx=F\left(x\right)\Rightarrow\int\limits^{17}_1f\left(x\right)dx=F\left(17\right)-F\left(1\right)\)
Từ giả thiết:
\(2x.f\left(x^2+1\right)+\dfrac{f\left(\sqrt{x}\right)}{2\sqrt{x}}=2lnx\)
Lấy nguyên hàm 2 vế:
\(F\left(x^2+1\right)+F\left(\sqrt{x}\right)=2xlnx-2x+C\)
Thay \(x=4\):
\(F\left(17\right)+F\left(2\right)=16ln2-8+C\) (1)
Thay \(x=1\):
\(F\left(2\right)+F\left(1\right)=-2+C\) (2)
Trừ vế cho vế (1) cho (2):
\(F\left(17\right)-F\left(1\right)=16ln2-6\)
Vậy \(\int\limits^{17}_1f\left(x\right)dx=16ln2-6\)

Mình thấy có phân biệt gì giữa hàm đa thức và phân thức đâu bạn.
Theo định nghĩa thì hàm đạt cực trị tại y'=0; đồng biến khi y' > 0 và nghịch biến khi y' < 0.
Cách làm bài hàm bậc 3 ở trên là chưa chính xác.
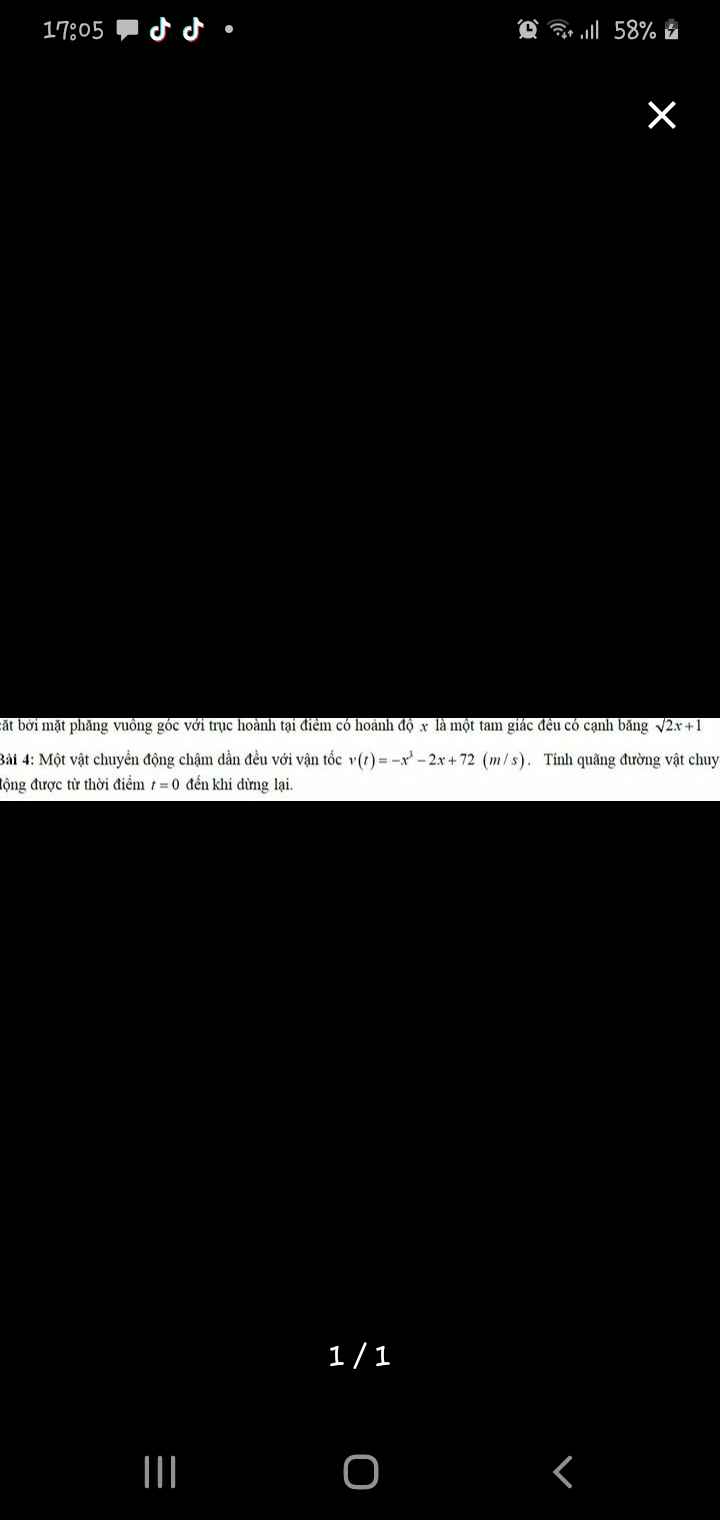 Em muốn hỏi là có thể gọi mấy cái x ở trong v (t) là ẩn t không ạ vì dạng này em thấy về ẩn t nên gặp cái ẩn x nó hơi hoang mang ạ nếu đc mn gthich cho em với ạ em cảm ơn 😢
Em muốn hỏi là có thể gọi mấy cái x ở trong v (t) là ẩn t không ạ vì dạng này em thấy về ẩn t nên gặp cái ẩn x nó hơi hoang mang ạ nếu đc mn gthich cho em với ạ em cảm ơn 😢


Đừng quan tâm cái \(k2\pi\) đi, lấy nghiệm là số cố định thôi. Ví dụ \(\cos x=1\) thì bạn tìm được dấu bằng xảy ra khi \(x=0\)
nghĩa là vứt luôn k2\(\pi\) ạ? chỉ ghi nghiệm là số đằng trước thôi ạ?